Given a sphere $S_k$ and a plane $P$
$$
\cases{
S_k\to (x-x_k)^2+(y-y_k)^2+(z-z_k)^2=r_k^2\\
P\to a x + b y + c z = d
}
$$
if $P$ and $S_k$ are tangent then eliminating $z$ we arrive at
$$
2 c z_k (a x+b y)+(a x+b y)^2+c^2 \left((x-x_k)^2+(y-y_k)^2+z_k^2-r_k^2\right)+d^2=2 d (a x+b y+c z_k)
$$
Solving for $y$ we have
$$
y = \frac{p_{1k}(x)\pm\sqrt{p_{2k}(x)}}{b^2+c^2}
$$
but as $S_k$ and $P$ are tangent we have necessarily
$$
p_{2k}(x) = 2 d (a x+b y_k+c z_k)-a^2 x^2-2 b y_k (a x+c z_k)+c \left(-2 a x z_k+c (r+x-x_k) (r-x+x_k)-c z_k^2\right)+b^2
\left(r^2-(x-x_k)^2-y_k^2\right)-d^2=0
$$
now solving for $x$ we have
$$
x = \frac{q_{1k}(x)\pm\sqrt{q_{2k}(x)}}{a^2+b^2+c^2}
$$
again due to tangency necessarily we have
$$
q_{2k}(x) = (a x_k + b y_k + c z_k - d)^2-(a^2 + b^2 + c^2) r_k^2 = 0
$$
Choosing now $a^2 + b^2 + c^2=1$ we have
$$
\cases{
(a x_k + b y_k + c z_k - d)^2-r_k^2 = 0, \ \ k = (1,2,3)\\
a^2 + b^2 + c^2=1
}
$$
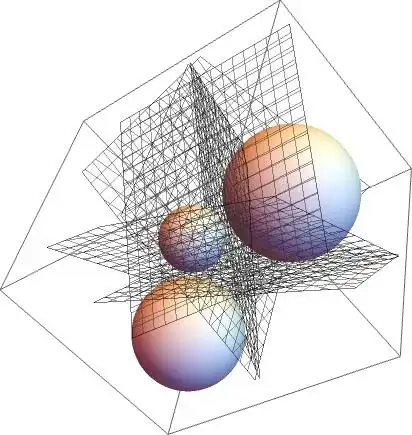
four equations and four unknowns $(a,b,c,d)$ and solving this equation system, we will obtain the sought planes. Attached a plot showing the case
$$
\cases{
S_1\to\ p_1 = (5,0,-1), \ r_1 = 3\\
S_2\to\ p_2 = (-4,-2,2), \ r_2 = 6\\
S_3\to\ p_3 = (8,-5,-7), \ r_3 = 5\\
}
$$