Update: complex numbers
This implementation with complex numbers seems to work for now
import math
import cmath
import numpy as np
'''
Algorithm for finding the coefficients of
the linear equations of the four tangent
lines of a pair of non-intersecting ellipses
'''
given a pair of conics, as a pair of symmetric matrices,
calculate the vector k = (k[0], k[1], k[2]) of values for each of which
the conic c1 - k[i]c2 from the pencil of conics c1 - tc2
is a degenerate conic (the anti-symmetric product of a pair of linear forms)
and also find the matrix U
of the projective transformation that simplifies the geometry of
the pair of conics, and the geometry of the pencil c1 - t*c2 in general,
as well as the geometry of the three degenerate conics in particular
def get_transformation(c1, c2):
'''
c1 and c2 are 3 by 3 symmetric matrices of the two conics
'''
c21 = np.linalg.inv(c2).dot(c1)
k, U = np.linalg.eig(c21)
return k, U
def find_common_points(c1, c2):
k, U = get_transformation(c1, c2)
L1 = (U.T).dot((c1 - k[0]c2).dot(U))
L2 = (U.T).dot((c1 - k[1]c2).dot(U))
x_0 = cmath.sqrt(-(L2[2,2] / L2[0,0]))
y_0 = cmath.sqrt(-(L1[2,2] / L1[1,1]))
sol = np.array([[ x_0, y_0, 1],
[-x_0, -y_0, 1],
[-x_0, y_0, 1],
[ x_0, -y_0, 1]])
sol = sol.dot(U.T)
return sol
combination of the algorithms form above with the
transformation of the problem of common tangents of the two ellipses
to its dual - the intersection points of the two dual ellipses
The intersection points of the dual ellipses
are the common tangents of the two original ellipses
def find_common_tangents(c1, c2):
dc1 = np.linalg.inv(c1)
dc2 = np.linalg.inv(c2)
return find_common_points(dc1, dc2)
Previous version: real version, non-intersecting ellipses
If an algorithm is what you are seeking, here is one, based on my previous posts you cited:
import math
import numpy as np
'''
Algorithm for finding the coefficients of
the linear equations of the four tangent
lines of a pair of non-intersecting ellipses
'''
given a pair of conics, as a pair of symmetric matrices,
calculate the vector k = (k[0], k[1], k[2]) of values for each of which
the conic c1 - k[i]c2 from the pencil of conics c1 - tc2
is a degenerate conic (the anti-symmetric product of a pair of linear forms)
and also find the matrix U
of the projective transformation that simplifies the geometry of
the pair of conics, and the geometry of the pencil c1 - t*c2 in general,
as well as the geometry of the three degenerate conics in particular
def get_transformation(c1, c2):
'''
c1 and c2 are 3 by 3 symmetric matrices of the two conics
'''
c21 = np.linalg.inv(c2).dot(c1)
k, U = np.linalg.eig(c21)
return k, U
find the common points, i.e. points of intersection,
of a pair of non-intersecting ellipses
represented by a pair of symmetric matrices
def find_common_points(c1, c2):
'''
c1 and c2 are 3 by 3 symmetric matrices of the two conics
'''
k, U = get_transformation(c1, c2)
L1 = (U.T).dot((c1 - k[0]c2).dot(U))
L2 = (U.T).dot((c1 - k[1]c2).dot(U))
sol = np.ones((4,3), dtype=float)
for i in range(2):
for j in range(2):
sol[i+2*j,0:2] = np.array([math.sqrt(abs(L2[2,2] / L2[0,0]))(-1)i, math.sqrt(abs(L1[2,2] / L1[1,1]))(-1)**j])
sol = sol.dot(U.T)
return sol
combination of the algorithms form above with the
transformation of the problem of common tangents of the two ellipses
to its dual - the intersection points of the two dual ellipses
The intersection points of the dual ellipses
are the common tangents of the two original ellipses
def find_common_tangents(c1, c2):
dc1 = np.linalg.inv(c1)
dc2 = np.linalg.inv(c2)
return find_common_points(dc1, dc2)
I tested it with one example, and it worked, but have not run more tests.
Here is a test script:
'''
Begin generation of test conics
'''
def cos_sin(angle_deg):
return math.cos(angle_degmath.pi/180), math.sin(angle_degmath.pi/180)
def rotation(cs_sn):
return np.array([[cs_sn[0], -cs_sn[1]],
[cs_sn[1], cs_sn[0]]])
def isom(angle, translation):
'''
#isometry from conic-aligned coordinate system (conic attached)
#to global coordinate system (world system)
isometry from global coordinate system (world system)
to conic-aligned coordinate system (conic attached)
'''
cos_, sin_ = cos_sin(-angle)
tr = - rotation((cos_, sin_)).dot(translation)
return np.array([[ cos_, -sin_, tr[0]],
[ sin_, cos_, tr[1]],
[ 0, 0, 1 ]])
def conic(major, minor, angle, center):
D = np.array([[minor**2, 0, 0],
[ 0, major**2, 0],
[ 0, 0, -(minormajor)*2]])
U = isom(angle, center)
return (U.T).dot(D.dot(U))
def conic_coeff(c):
return np.array( (c[0,0], 2c[0,1], c[1,1], 2c[0,2], 2*c[1,2], c[2,2]) )
'''End generation of test conics'''
BEGIN test:
rnd=5 # rounding to 5 digits after the decimal point. Choose as you like.
a = 2
b = 1
cntr = np.array([0,0])
w = 45
C1 = conic(a, b, w, cntr)
Eq1 = conic_coeff(C1).round(rnd)
a = 3
b = 1
cntr = np.array([7,0])
w = 120
C2 = conic(a, b, w, cntr)
Eq2 = conic_coeff(C2).round(rnd)
common_tangents = find_common_tangents(C1, C2)
print()
print('equation of the conic 1:')
print(f'{Eq1[0]}x2 + {Eq1[1]}xy + {Eq1[2]}y2 + {Eq1[3]}x + {Eq1[4]}y + {Eq1[5]} = 0')
print()
print('equation of conic 2:')
print(f'{Eq2[0]}x2 + {Eq2[1]}xy + {Eq2[2]}y2 + {Eq2[3]}x + {Eq2[4]}y + {Eq2[5]} = 0')
print()
print('The coefficients of the linear equations of the four tangent lines to the conics 1 and 2 are: ')
print(common_tangents.round(rnd))
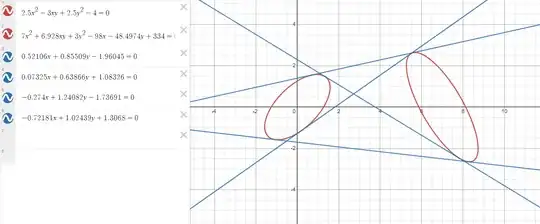
After running this particular test, I got as output:
equation of conic 1:
2.5x**2 + -3.0xy + 2.5y**2 + 0.0x + 0.0y + -4.0 = 0
equation of conic 2:
7.0x2 + 6.9282xy + 3.0y2 + -98.0x + -48.49742y + 334.0 = 0
the coefficients of the linear equations of the four tangent lines to the conics 1 and 2 are:
[[ 0.52106 0.85509 -1.96045]
[ 0.07325 0.63866 1.08326]
[-0.274 1.24082 -1.73691]
[-0.72181 1.02439 1.3068 ]]
Then I went to Desmos, because I find it convenient, and plotted the output, just to check visually:


E0: 36.0 * x^2 + -0.0 * x * y + 9.0 * y^2 + 0.0 * x + 0.0 * y + -324.0 = 0andE1: 4.0 * x^2 + -0.0 * x * y + 1.0 * y^2 + -56.0 * x + -6.0 * y + 201.0 = 0Considering the method I described in my question, please can you explain how you get the four tangents final equations. Super thanks for your help.
– MohG Oct 18 '23 at 12:45