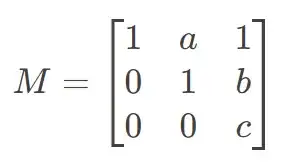0

For which, if any, values of $a,b,c \in \mathbb{R}$ is the matrix

enter image description here

diagonalizable?

The Eigenvalues are easy enough. I get $\lambda=1$ (With an algebraic multiplicity of $2$) and $\lambda=c$ (With an algebraic multiplicity of $1$). I'm not really sure how to proceed though.

I could get the eigenvectors by imposing restrictions on the eigenvalues but that's a very painful process and I am not sure if this is the best way too approach this... Any suggestions?

Future Math person
  • 2,937
  • Check first the geometric multiplicity of $\lambda=1$. – CroCo Aug 17 '23 at 09:28
  • See this duplicate (works the same way). – Dietrich Burde Aug 17 '23 at 09:28
  • A diagonalizable matrix has the geometric multiplicity of $\lambda$ be equal to the algebraic multiplicity. The easiest way to calculate is to check if the rank of $M - \lambda I$ (the number of linearly independent columns or rows of $M - \lambda I$) is equal to $n$ minus the algebraic multiplicity of $\lambda$, where $n = 3$ is the dimension of the $M$, and $\lambda$ goes over the distinct eigenvalues of $M$. – user3257842 Aug 17 '23 at 09:32
  • @user3257842 I was going to answer but your comment beats me. Please convert the comment to an answer noting that a nonzero matrix has rank 1 iff each row is a multiple of one of them. – Oscar Lanzi Aug 17 '23 at 10:37

1 Answers1

1

Find the minimal polynomial of $M$. $M$ will be diagonalisable if and only if the minimal polynomial is a product of linear factors.

Sudhir Kumar
  • 31