0

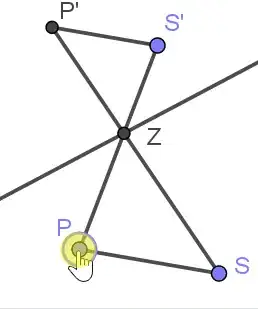
A construction is as follows:

Given a fixed line $L$ and two fixed points $S,S'$.
For any point $P$ on the plane, let the line $PS'$ intersect $L$ at $Z$.
Draw the line through $S'$ parallel to $SP$, intersecting the line $SZ$ at $P'$.
The map $P\mapsto P'$ maps lines through $S$ to parallel lines through $S'$: the line $S'P'$ is parallel to $SP$.
enter image description here

By composing with a translation, we can assume $S=S'$.

then I try to describe the matrix of projective transformations on $\mathbb RP^2$ that fix the point $[0,0,1]$, and fixes any line through $[0,0,1]$.

I verified that any projective transformation represented by $$\pmatrix{1&0&0\\0&1&0\\A&B&C}$$ where $A,B,C\in\Bbb R,C\ne0$ satisfies the condition. Is that all of them?

To verify it satisfies the condition:
Compute the adjugate matrix is $\left( \begin{array}{ccc} C & 0 & 0 \\ 0 & C & 0 \\ -A & -B & 1 \\ \end{array} \right)$.
Any line through $[0,0,1]$ is of the form $[u,v,0]$. $$(u,v,0)\left( \begin{array}{ccc} C & 0 & 0 \\ 0 & C & 0 \\ -A & -B & 1 \\ \end{array} \right)=(Cu,Cv,0)$$ so the line $[u,v,0]$ is fixed.

hbghlyj
  • 5,361

1 Answers1

0

Since the projective transformation $T$ fixes $[0,0,1]$, it is of the form $$\left( \begin{array}{ccc} a_{11} & a_{12} & 0 \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & C \\ \end{array} \right)$$ The adjugate matrix is $$\left( \begin{array}{ccc} a_{22} C &-a_{12}C & 0 \\ -a_{21}C& a_{11} C & 0 \\ a_{21} a_{32}-a_{22} a_{31} & a_{12} a_{31}-a_{11} a_{32} & a_{11} a_{22}-a_{12} a_{21} \\ \end{array} \right)$$ $T$ fixes the line $[1,0,0]$, then $\mathrm{adj}(T)$ has a left-eigenvector $(1,0,0)$ $$(1,0,0)\left( \begin{array}{ccc} a_{22} C & a_{12} (-C) & 0 \\ a_{21} (-C) & a_{11} C & 0 \\ a_{21} a_{32}-a_{22} a_{31} & a_{12} a_{31}-a_{11} a_{32} & a_{11} a_{22}-a_{12} a_{21} \\ \end{array} \right)=\left(a_{22} C,-a_{12} C,0\right)$$ so $a_{12}=0$.

Similarly, $T$ fixes the line $[0,1,0]$, then $a_{21}=0$.
Now the matrix of $T$ becomes $$\left( \begin{array}{ccc} a_{11} & 0 & 0 \\ 0 & a_{22} & 0 \\ a_{31} & a_{32} & C \\ \end{array} \right)$$ The adjugate matrix is $$\left( \begin{array}{ccc} a_{22} C & 0 & 0 \\ 0 & a_{11} C & 0 \\ -a_{22} a_{31} & -a_{11} a_{32} & a_{11} a_{22} \\ \end{array} \right)$$ $T$ fixes the line $[u,v,0]$, then $\mathrm{adj}(T)$ has a left-eigenvector $(u,v,0)$ $$(u,v,0)\left( \begin{array}{ccc} a_{22} C & 0 & 0 \\ 0 & a_{11} C & 0 \\ -a_{22} a_{31} & -a_{11} a_{32} & a_{11} a_{22} \\ \end{array} \right)=\left(a_{22} C u,a_{11} C v,0\right)$$ so $a_{11}=a_{22}$. The matrix of $T$ becomes $$\left( \begin{array}{ccc} a_{11} & 0 & 0 \\ 0 & a_{11} & 0 \\ a_{31} & a_{32} & C \\ \end{array} \right)$$ Since $T$ is non-singular, $a_{11}\ne0$.
Multiply by a scalar $a_{11}^{-1}$ we finally see $T$ is of the form$$\pmatrix{1&0&0\\0&1&0\\A&B&C}$$

hbghlyj
  • 5,361