I made a sequence related to prime numbers.
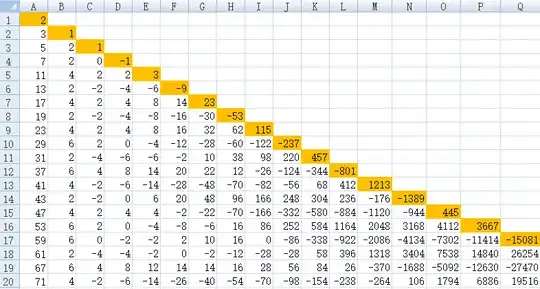
In column A, I listed the sequence of prime numbers.
In column B, I listed the sequence of gaps between the prime numbers.
In column C, I listed the sequence of gaps between the terms of the previous sequence.
In column D, I listed the sequence of gaps between the terms of the previous sequence.
And so on.
I took the terms in the top diagonal (highlighted above; A007442 and also here), took the logs of their absolute values, and called this new sequence $u_n$.
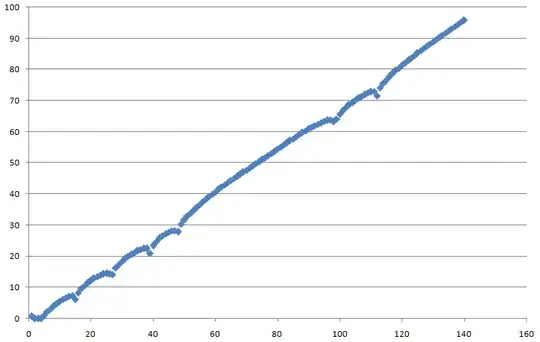
Here is a graph of $u_n$ against $n$:
There are strange dips in the graph. The dips do not appear suddenly, but rather at the end of distinct arcs.
The coordinates of the first few dips are:
$(15, 6.10)$
$(27,14.27)$
$(39,20.98)$
$(48,27.84)$
$(98,63.25)$
$(112, 71.61)$
Is there any explanation for this pattern?
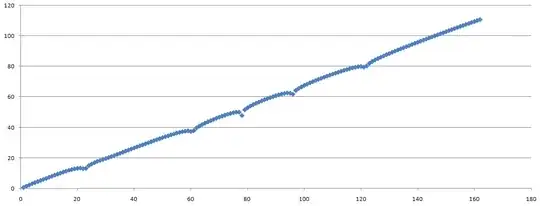
Note that this kind of pattern is not unique to the sequence of prime numbers. The sequence of prime numbers is just a good example. Another example: in column A, I replaced the sequence of prime numbers with the digits in the decimal expansion of $e$ (A001113), and got the following graph, which also has dips:
It seems that, to produce a graph with dips, the sequence in column A must have some kind of irregularity.