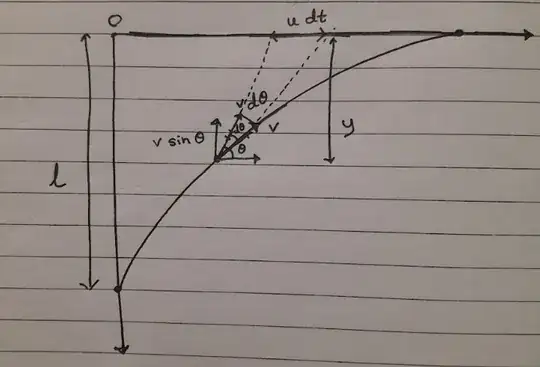
A cat moves along the x-axis with a uniform velocity u. A dog moves with a uniform speed $v$ such that at every moment it is aimed towards the cat. Initially, at $t = 0$, the dog is perpendicular to the cat at a distance $l$ away from it. Find the equation of the trajectory of the dog.
My Approach:
(I used a hand-drawn diagram because I can't draw digitally)
Suppose the dog has a velocity $v$ at a given instant (say at time $t$). Now, its velocity vector shifts as shown in the figure after a time $dt$ when the cat travels a distance $u$ $dt$. Now, clearly these shown triangles are similar. Thus, we get $$\frac{v \space \sin \theta}{y} = \frac{v \space d\theta}{u \space dt}$$ $$\implies dt = \frac{y \space d\theta}{u \space \sin \theta}$$ Now, we know, $$dy = v \space \sin \theta \space dt$$ $$\implies dy = v \space \sin \theta \space \frac{y \space d\theta}{u \space \sin \theta}$$ $$\implies \frac{dy}{y} = \frac{v \space d\theta}{u }$$ $$\implies \int_{l}^{y} \frac{dy}{y} = \int_{\frac{\pi}{2}}^{\theta} \frac{v \space d\theta}{u }$$ $$\implies \ln( \frac{y}{l}) = \frac{v \space (\theta - \frac{\pi}{2} )}{u }$$ $$\therefore y = l\space e^{\frac{v \space (\theta - \frac{\pi}{2})}{u }}$$ Now, I tried using the fact that $\frac{dy}{dx} = \tan \theta$ but the expression I obtained for $x$ in terms of $\theta$ was not something I could integrate. Please suggest how to compute for $x$ and if this flow of logic is correct.