2

In the following I will use definitions and constructions of simplicial complexes and $\Delta$-complexes/sets from Greg Friedman's An elementary illustrated Introduction to simplicial sets.

I'm looking for an example of a $\Delta$-complex which cannot be endowed with structure of a simplicial complex or a proof that it always works. In this case one should say this space is "triangulable".

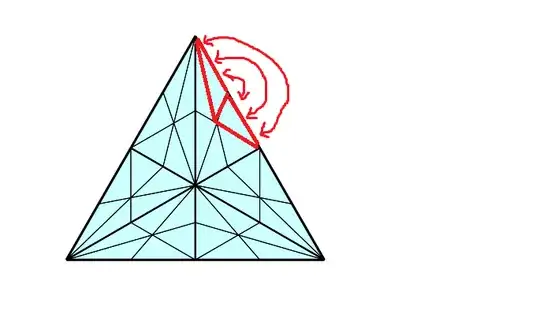
Note that of course it's easy to construct a $\Delta$-complex which isn't a simplicial complex with respect the choices of simplices comming from the $\Delta$-complex datum: see example on page 11 in Friedman's notes. And this should be not surprising at all because $\Delta$-complexes allow much more flexibility in gluing boudaries than simplicial complex. But that's not what I'm asking about: if we subdivide the $2$-cell in tree new $2$-cells, then we can endow this $\Delta$-complex with another simplex structure which turns it into a honest simplicial complex.

And so my question is if every $\Delta$-complex "triangulable" in the sense that one can endow it with structure of a simplicial complex (ie decompose it into simplices satisfying glueing relations allowed for simplicial complex) which might have nothing to do with original $\Delta$-complex structure?

Supplemental picture:

enter image description here

user267839
  • 9,217
  • The word you are looking for is "triangulable", as written on the page you cite. The geometric realisation of any simplicial set – hence also any $\Delta$-set – is triangulable, by subdividing twice. – Zhen Lin Jan 22 '23 at 22:19

1 Answers1

3

Here is an exercise: The 2nd barycentric subdivision of every $\Delta$-complex is a simplicial complex.

To follow up on our discussion in the comments, let me address the example edited in to your post.

Let me denote the large blue $2$-simplex as $\Sigma$, which we think of as the domain of one of the simplices in the given $\Delta$-complex $X$, with corresponding characteristic map denoted $f : \Sigma \to X$.

Let me also denote the highest vertex of $\Sigma$ as $A$, the lower right vertex of $\Sigma$ as $E$, and all the other vertices of the 2nd barycentric subdivision along $\overline{AE}$ as $A,B,C,D,E$.

A key observation here is that while it is possible that $f(A)=f(E)$, there is no other possibility of two points on $\overline{AE}$ being mapped to the same image by $f$: the function $f$ is injective on the half-open edge $[A,E)$. This follows from the definition of a $\Delta$-complex, together with the assumption that $f$ is one of the characteristic maps of the given $\Delta$-complex.

Consider also the two red outlined 2-simplices in your diagram, each of which is a simplex of the 2nd barycentric subdivision of $\Sigma$; let me denote them as $\sigma$, which has $\overline{AB}$ as one of its edges, and $\tau$ which has $\overline{BC}$ as one of its edges. Notice that $\sigma \cap \tau$ is a common $1$-simplex face of each of $\sigma$ and $\tau$.

The thing to observe is that $f$ is injective on $\sigma$, also $f$ is injective on $\tau$, and finally $f(\sigma) \cap f(\tau) = f(\sigma \cap \tau)$. This holds because $f$ is injective on $[A,C)$.

Lee Mosher
  • 135,265
  • When we perform the first subdivision we obtain a $\Delta$-complex such that in every simplex the vertices are different. (because by def of $\Delta$-complex the intersection of the inner $\overset{\circ}{\Delta_k }$ of any $k$-simplex $\Delta_k$ with any $(k-1)$-simplex must be trivial) What I not understand why after second subdivision we obtain a simplicial complex? One of the central features of´simplicial complexes is that every simplex is uniquely determined by it's vertices. – user267839 Feb 11 '23 at 21:49
  • But I not see why after second subdivision we cannot obtain a complex containing two distinct simplices having identical vertices. Could you give a hint how to resolve this problem? – user267839 Feb 11 '23 at 21:49
  • 1
    Here's a hint: Do a proof by induction on the dimension of the skeleta $X^{(k)}$ of the given $\Delta$ complex $X$. First prove that the second barycentric subdivision of $X^{(0)}$ is a simplicial complex (this is obvious). Then, assuming that the second barycentric subdivision of $X^{(k)}$ is a simplicial complex, prove that the second barycentric subdivision of $X^{(k+1)}$ is a simplicial complex. – Lee Mosher Feb 12 '23 at 00:21
  • There is one point I'm not sure about how to resolve it. Pick a $(k+1)$-simplex $\Delta_{k+1}$ and perform two barycentric subdivisions on it and assume that we already know that the $k$ skeleton $X^k$ is already simplicial complex. Then we obtain $(k+1)^2$ new $(k+1)$-simpleces. – user267839 Mar 07 '23 at 00:48
  • The difference between a $\Delta$- and a simplicial complex is that of the latter there are two additional glueing rules: 1) all vertices of a simplex are different 2) any two simplices share at most one common lower simplex as intersection. Clearly 1) is satisfied because if there is a new $(k+1)$-simplex having two or more identified vertices by construction it's $k$-face which contains these vertices is contained in $k$-face of initial $(k+1)$-simplex $\Delta_{k+1}$, so we are inside $k$-skeleton $X^k$. We conclude by induction that all vertices of $k$-face are different. – user267839 Mar 07 '23 at 00:48
  • Now the PROBLEM: To check the point 2) about which I'm asking is a bit more delicate and I not know how to continue: Say we consider two new $(k+1)$-simplices $\Delta_{k+1}', \Delta_{k+1}''$ obtained from subdividing $\Delta_{k+1}$ and having following property: they are "neighbours in the sense that they share a common $k$-face beeing contained in the inner of $\Delta_{k+1}$ (ie a brand new $k$-simplex which the old complex not see) and each of them has at least one $k$-face $\Delta_k', \Delta_k''$ beeing contained in the $k$-face of the old simplex $\Delta_{k+1}$. – user267839 Mar 07 '23 at 00:49
  • How to show that it is NOT possible that these $k$-faces $\Delta_{k}', \Delta_{k}'' \subset \partial \Delta_{k+1}$ of these two new $(k+1)$-simplices $\Delta_{k+1}', \Delta_{k+1}''$ lying on the $k$-face of $\Delta_{k+1}$ can appear to be glued together in the resulting complex? Which rule would in case of existence of such glueing configuration be violated. – user267839 Mar 07 '23 at 00:55
  • The particular details of barycentric subdivision are important for this problem, and perhaps it'll help to ponder those details. For example, under barycentric subdivision, a $k+1$ simplex is subdivided into $(k+2)!$ distinct $k+1$ simplices (not $k+1$ of them), and under 2nd barycentric subdivision it is subdivided into $((k+2)!)^2$ distinct $k+1$ simplices (not $(k+1)^2$). So for example a $2$-simplex is subdivided into $(3!)^2 = 36$ distinct $2$-simplices under 2nd barycentric subdivision. Thinking hard about the $1$-skeleton, and next about the $2$-skeleton, would be helpful too. – Lee Mosher Mar 07 '23 at 02:44
  • Yes sorry, I confused the number of simplices into which the barycentric division splits. But the problem stays the same. To clarify to problem I'm still struggling with I added a picture of a $2$-simplex (let call it as before $\Delta_{2}$) subdivided via the b.d. and the problem I tried to explain in previous comment concerns the two marked in red $2$-simplices, call them $\Delta_{2}', \Delta_{2}''$. Assume we start with a $\Delta$-complex containing this $2$-simplex (before subdivision). – user267839 Mar 08 '23 at 00:17
  • Especially, that means that in the $1$-skeleton of the complete complex the boundaries could be subjected to certain strange gluings. – user267839 Mar 08 '23 at 00:19
  • Now the goal is to show that the only simplex lying in the intersection $\Delta_{2}' \cap \Delta_{2}''$ of the new complex obtained from 2x bs is the new $1$-simplex in the inner of $\Delta_{2}$ and we want to avoid the scenrio that the $1$-faces of $\Delta_{2}' $ and $ \Delta_{2}''$ which are lying on the boundary of $\Delta_{2}$ can be become glued together. (This would imply that the intersction $\Delta_{2}' \cap \Delta_{2}''$ would be consist of TWO! $1$-simplices, and therefore the new complex would not be simplicial.) Do you see how to argue that such scenario cannot appear? – user267839 Mar 08 '23 at 00:19
  • That's the only pathology I can't still resolve. – user267839 Mar 08 '23 at 00:21
  • I added some to my answer to address your latest coments. – Lee Mosher Mar 08 '23 at 01:05
  • Thank you a lot. This uncovers exactly the point I missed to exploit in my considerations : for every simplex $\Delta_k $ beeing part of a $\Delta$- complex $X$ the inner $\overset{\circ}{\Delta_k} $ is embedded, so there are no additional identifications in the inner allowed when we consider this $k$-simplex individually as subset of $X$. That's what you apply above to $1$-simplex $AE$. Thank you for explanation, I understand it now – user267839 Mar 08 '23 at 13:23