17

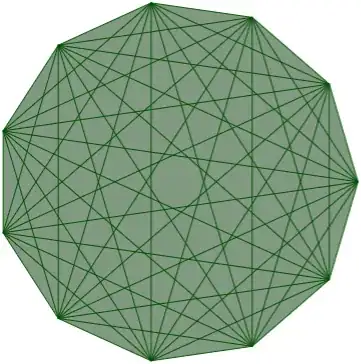
Consider a regular $n$-gon of side length $1$ with its diagonals. Here is an example with $n=11$ (from geogebra applet).

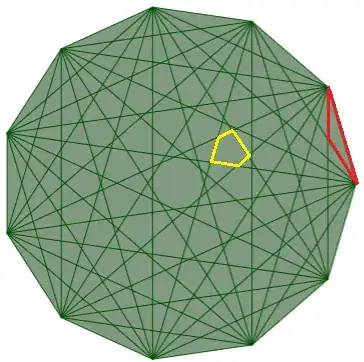
enter image description here

Excluding the centre cell when $n$ is odd, I've been trying to find bounds on the area of the largest cell, in terms of $n$.

It seems that, for every value of $n$, the largest non-centre cell has roughly similar area as the outermost cell, whose area is $\frac{1}{4}\tan{\frac{\pi}{n}}\approx\frac{\pi}{4n}$.

enter image description here

That is, $(\text{area of largest non-centre cell})\approx\frac{\pi}{4n}$. (This claim has strong numerical evidence.)

My question is:

In a regular $n$-gon of side length $1$ with diagonals, what is the infimum and supremum of $n\times(\text{area of largest non-centre cell})$ ?

(The number of cells is approximately $\frac{1}{24}n^4$ for large $n$.)

Dan
  • 35,053
  • I believe the area of each cell bordering an edge of the polygon is also $\frac{\pi}{4n}(1+o(1))$. So the claim is tantamount to the claim that no interior region has area much smaller than those regions. – Carl Schildkraut Dec 16 '22 at 22:23
  • @CarlSchildkraut I'm not sure I follow. The claim (that area of largest non-centre region is $\frac{\pi}{4n}(1+o(1))$) does not say something about all the interior regions; it just says something about the largest non-centre interior region. – Dan Dec 16 '22 at 22:49
  • Sure, but this provides a lower bound: there exists a non-center interior region with area $\frac{\pi}{4n}(1+o(1))$. – Carl Schildkraut Dec 16 '22 at 23:59
  • 1
    Posted on MO. – Dan Dec 17 '22 at 13:24

0 Answers0