A question on integrating a function, with respect to another function?

Question

I've been asked to find the area described by $$A={ (x,y), y^2 \leqslant2x; and, y\geqslant 4x-1 } $$ which is effectively the following area(If I can insert a graph using mathJax, please let me know in the comments)

The area is the area that's shaded both blue and red

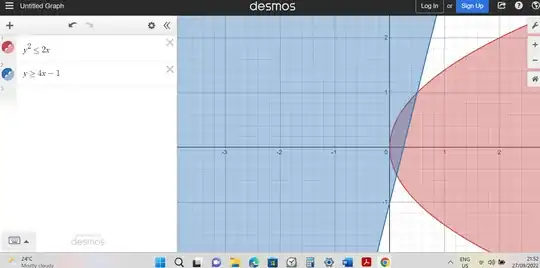
The normal way to find this is to set up multiple integrals that remove undesired areas, however, this method requires one to be hyperattentive of what they're doing, so I was thinking of integrating let's say the equation $y^2=2x$ , with respect to $y=4x+1$ , with the bounds being the points at which the line intersects the parabola. Thus, the integral would be

$$\int_{0.125}^{0.5} \sqrt{2x} {d({4x-1)}}$$ which is the same as $$ 4 \int \sqrt{2x} dx$$, when evaluated as an indefinite integral

I'm hoping the above step "transforms" the graph(sorry if the terminology is wrong)

the new bounds of the integral as given by $4x-1= 0.125$ which implies the lower limit is $0.28125$ , and the upper limit $0.375$

thus the new integral is $$ 4 \int_{0.02815}^{0.375} \sqrt{2x} dx$$

I have come across answers like this on integrating one function, with respect to another, however, the way they have done the u-sub there is confusing me, so I'm asking this as a new question, this time with the primary point of interest being areas

Is this conceptually right, and if not, where am I going wrong?

footnote:- For those interested, this problem is from the 2015 JEE mains paper, a competitive engineering entrance exam in India. I'm aware that solutions are available online, but I wanted to know if this approach is correct.

The best I can say is that I think this is accidentally right. If you try this technique on another pair of intersecting curves I don't think you'll get the same answer. — Matthew Leingang, Sep 27 '22 at 16:58
I think his would only work if I were to find the area between a line and a curve, right? — math and physics forever, Sep 27 '22 at 16:59
By the way, what I would call the “normal” way to do this problem is to integrate vertically. The difference of the $x$-coordinates is $(y+1)/4 - y^2/2$, and the limits of integration are the $y$-coordinates of the intersections. — Matthew Leingang, Sep 27 '22 at 17:08
Yeah, I understand that, but I still have to subtract regions, which is what I want to avoid — math and physics forever, Sep 27 '22 at 17:12
But in what situations could multiplying take the place of subtracting? This is my biggest concern with your method. — Matthew Leingang, Sep 27 '22 at 17:16
Where did I multiply? I multiplied because of the differential element — math and physics forever, Sep 27 '22 at 17:17
In my answer, the differential element, was 4x-1 which is why I multiplied by 4 — math and physics forever, Sep 27 '22 at 17:27
As this question hasn't received any answers yet, I'll be offering a bounty on it shortly, so even if you have an answer, please wait until I offer the bounty so that you can claim the same — math and physics forever, Sep 29 '22 at 13:39
It has been suggested that you try it with a different example. Why haven't you taken this excellent advice? — Gerry Myerson, Sep 30 '22 at 23:26
When a method works, it makes sense to ask why it works, that is, to ask for a proof. When a method doesn't work, it's generally because there was no good reason to expect it would work, and that's about all one can say. — Gerry Myerson, Oct 01 '22 at 23:31

A question on integrating a function, with respect to another function?

0 Answers0