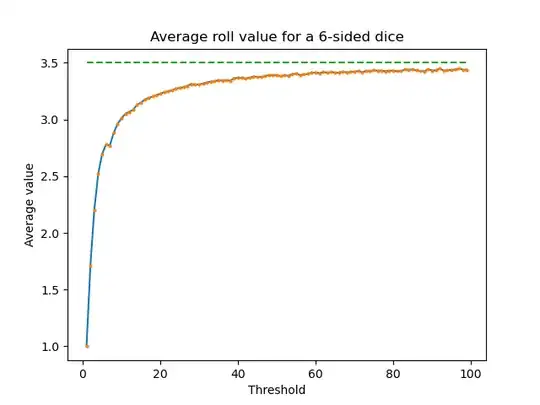
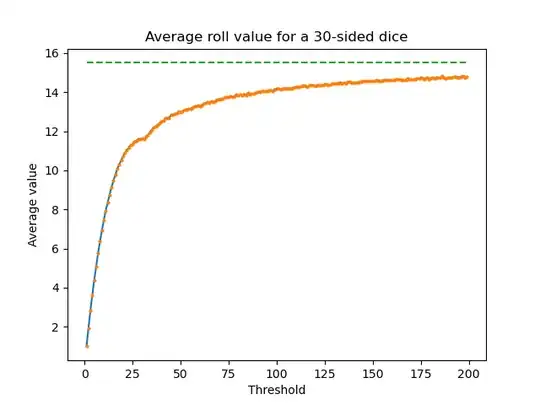
Sketch for an analytical solution: you are asking for the expectation related to something that in probability theory is named an stopping time related to an stochastic process, i.e., related to a sequence of random variables.
Let $\{X_n\}_{n\in\mathbb{N}}$ a sequence of i.i.d. random variables, where each $X_k$ represents a dice, and set $T:=\min\{n: S_n\geqslant t\}$ for some fixed $t>0$ (the threshold), where $S_n:=\sum_{k=1}^n X_k$. Then $T$ is the number of throws where you reach the threshold.
Now suppose that $T=n$, that is, we have that $S_n\geqslant t$ but $S_{n-1}<t$. This means that $S_n=t+k$ for some $k\in\{0,\ldots ,s-1\}$, being $s$ the number of sides of the dice. In this case you will have that the mean value of the dice will be just $t/n$, as we discard the value of $k$ every time, therefore we want to compute
$$
\sum_{n\geqslant 1}\frac{t}{n}P(T=n)=t \sum_{n\geqslant 1}\frac1{n}P(T=n)=t\, \mathrm{E}[1/T]\tag1
$$
Now we can use the following result to approach $\mathrm{E}[1/T]$: suppose that $g:[a,\infty )\to \mathbb{R}$ is continuously differentiable and monotonic, and that $\operatorname{supp}(X)\subset [a,\infty )$, then
$$
\begin{align*}
\mathrm{E}[g(X)]&=\int_{[a,\infty )}g(t)P_X(dt)\\
&=\int_{[a,\infty )}(g(t)+g(a)-g(a))P_X(dt)\\
&=\int_{[a,\infty )}\left(\left(\int_{[a,t]}g'(s)\,d s\right)+g(a)\right)P_X(dt)\\
&=g(a)+\int_{\{(s,t):a\leqslant s\leqslant t\}}g'(s)\,d s \otimes P_X(dt)\\
&=g(a)+\int_{[a,\infty )}g'(s)P(X\geqslant s)\,d s\tag2
\end{align*}
$$
where we used Tonelli's theorem in the last two equalities. In our case first note that
$$
\{T\geqslant r\}=\{T\geqslant \lceil r \rceil \}=\{S_{\lceil r \rceil -1}<t\}=\{S_{\lceil r\rceil-1 }\leqslant \lceil t-1\rceil \}\tag3
$$
Then using (2) and (3) we reach the identity
$$
\begin{align*}
\mathrm{E}[1/T]&=1-\int_{[1,\infty )}\frac1{r^2}P(T\geqslant r)\,d r\\
&=1-\int_{[1,\infty )}\frac1{r^2}P(T\geqslant \lceil r \rceil )\,d r\\
&=1-\int_{[1,\infty )}\frac1{r^2}P(S_{\lceil r \rceil -1 }\leqslant \lceil t-1 \rceil )\,d r\\
&=1-\sum_{n\geqslant 1}P(S_n\leqslant \lceil t-1 \rceil )\int_{[0,1]}\frac1{(n+s)^2}\,d s\\
&=1-\sum_{n\geqslant 1}P(S_n\leqslant \lceil t -1\rceil )\frac{1}{n(n+1)}\\
&=1-\sum_{n=1}^{\lceil t -1\rceil }P(S_n\leqslant \lceil t-1 \rceil )\frac{1}{n(n+1)}\tag4
\end{align*}
$$
(Note that (4) can be derived more straightforwardly from (1) using summation by parts.)
I'm not sure if this is the more simple or useful approach to the problem, besides a Montecarlo simulation. Anyway the distribution of each $S_n$ for large $n$ can be approximated well by a normal distribution, so we can get some bounds for $\mathrm{E}[1/T]$. For an explicit computation of the cumulative distribution of each $S_n$ take a look here.