9

What is the exact value of the following limit?

$$L=\lim_{n\to\infty}\left(\frac{n}{2}+\min_{x\in\mathbb{R}}\sum_{k=0}^n{\cos(2^k x)}\right)$$

Experimenting on desmos suggests the following claims:

$\sum_{k=0}^n{\cos{(2^k x)}}$ is minimized when $x\approx \left(2m\pm\dfrac{2}{3}\right)\pi,m\in\mathbb{Z}$, with the approximation approaching equality as $n\to\infty$

$L\approx -0.704$

I do not know how to prove these claims.

(This question was inspired by another question.)

Dan
  • 35,053
  • 1
    Do you want absolute values around those cosines? The question you link to, and its relative at https://math.stackexchange.com/questions/306728 , suggests so. – David E Speyer Jul 29 '22 at 01:33
  • @DavidESpeyer No absolute value signs for this question, thanks. (My use of the phrase "inspired by" allows for significant deviation.) – Dan Jul 29 '22 at 01:43
  • 1
    I just wanted to point out Dap's very nice answer here https://math.stackexchange.com/a/2638656/448 . Adapting Dap's approach, if $\cos(x) \leq -1/2$ then $\cos(x) + \cos(2x) \geq -1$, so we can "amortize" all but possibly the last term and show that $\sum_{k=0}^n \cos(2^k x) \geq -n/2 -1$. – David E Speyer Aug 01 '22 at 15:05

2 Answers2

4

Long comment. I believe this type of question is extremely hard, if not impossible by the current technology, to answer. However, let me share some observation.

Define $\varphi_n$ by the $n$th sum:

$$ \varphi_n(x) = \frac{n}{2} + \sum_{k=0}^{n} \cos(2^k x) $$

We will consider the behavior of $\varphi_n (x)$ near $x = \frac{2\pi}{3}$.

\begin{align*} \varphi_n\left(\frac{2\pi}{3} + (-1)^n \frac{x}{2^n} \right) &= \frac{n}{2} + \sum_{k=0}^{n} \cos\left(\frac{2^{k+1}\pi}{3} + (-1)^n \frac{x}{2^{n-k}}\right) \\ &= \frac{n}{2} + \sum_{k=0}^{n} \left[ -\frac{1}{2}\cos\left(\frac{x}{2^{n-k}}\right) + (-1)^{n-k+1}\frac{\sqrt{3}}{2}\sin\left(\frac{x}{2^{n-k}}\right) \right] \\ &= -\frac{1}{2} + \sum_{k=0}^{n} \left[ \sin^2\left(\frac{x}{2^{n-k+1}}\right) + (-1)^{n-k+1}\frac{\sqrt{3}}{2}\sin\left(\frac{x}{2^{n-k}}\right) \right] \\ &= -\frac{1}{2} + \sum_{j=0}^{n} \left[ \sin^2\left(\frac{x}{2^{j+1}}\right) + (-1)^{j+1}\frac{\sqrt{3}}{2}\sin\left(\frac{x}{2^{j}}\right) \right] \\ &= -\frac{1}{2} + 2 \sum_{j=0}^{n} \sin\left(\frac{x}{2^{j+1}}\right)\sin\left(\frac{x}{2^{j+1}}+(-1)^{j+1}\frac{\pi}{3}\right). \end{align*}

Using this, define $\psi(x)$ by

$$ \psi(x) = -\frac{1}{2} + 2 \sum_{j=0}^{\infty} \sin\left(\frac{x}{2^{j+1}}\right)\sin\left(\frac{x}{2^{j+1}}+(-1)^{j+1}\frac{\pi}{3}\right). $$

Since $\varphi_n \bigl( \frac{2\pi}{3} + (-1)^n \frac{x}{2^n} \bigr)$ converges locally uniformly to $\psi(x)$ on $\mathbb{R}$, it follows that

$$\inf_{x\in\mathbb{R}} \psi(x) \geq \limsup_{n\to\infty} \left( \min_{x\in\mathbb{R}} \varphi_n(x) \right). $$

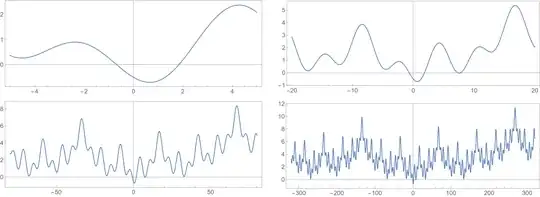
A numerical calculation suggests that $L = \inf \psi$ with an approximate value

$$\inf \psi \approx -0.70399210451640656752$$

at $x \approx 0.66123108104874561312$. Unfortunately, all the inverse symbolic calculators I tried could not identify this value. My gut is also telling that $L$ has no elementary closed-form, but again, this is rather a bold claim.

For fun, I included the graph of $\psi$:

graph of psi

Sangchul Lee
  • 181,930
  • +1 Thank you, that is a very valuable "comment". You mentioned "this type of question" - I wonder what you have in mind. Would Closed for of negative root of $x+x^2+x^4+x^8+...=0$ be another example of this type of question? – Dan Jul 28 '22 at 23:08
  • 2
    @Dan, Yes, that is another example. Also, finding $$\liminf_{x\to1^-}\sum_{n=0}^{\infty}(-1)^n x^{2^n}\qquad\text{and}\qquad\limsup_{x\to1^-}\sum_{n=0}^{\infty}(-1)^n x^{2^n}$$ is yet another problem of similar kind. We can prove that these are different. We can even give a smooth function that parametrizes all the limit points, yet finding the maximum/minimum sounds quite hard, if not impossible. – Sangchul Lee Jul 29 '22 at 19:48
0

This is far from an answer. The goal is to simplify the expression and to connect this problem with ergodic theory. We first note that w.l.o.g, we can assume $x\in[0,\pi]$. Denote $y=x/\pi$. Let the binary expansion of $y$ be $0.y_{1}y_{2}…y_{k}…$ (we exclude the expansion ending with all $0$ to make it unique). Then some algebra will show for $k\geq 1$ $cos(2^ky\pi)=cos(2*(0.y_{k}y_{k+1}…)*\pi)$.

Now let us define a few maps. Let $G$ maps $y\in[0,1]$ to the spaces of sequences (with each entry being either 0 or 1) $(y_{1},y_{2},……)$ using the binary expansion and let $G^{-1}$ be the inverse. Then define the Bernoulli shift $T$ on $(y_{1},y_{2},……)$ by $T(y_{1},y_{2},……)= (y_{2},y_{3},……)$

Finally, $\frac{1}{n}\sum_{k=1}^{k=n}cos(2^kx)=\frac{1}{n}\sum_{k=1}^{k=n}cos(2\pi G^{-1}T^{k-1}Gy)$. Then by using the Birkhoff ergodic theorem, for almost all $y$, the above converges to $\int_{0}^{1}cos(2\pi t)dt = 0$. But for $ y=\frac{2}{3}=0.101010…$, an explicit calculation shows that in this special case, the limit is $-\frac{1}{2}$

puppyHuazai
  • 250
  • Hey @puppyHuazai :) I don't understand the last two sentences. If $y=\frac 23=0.1010\cdots$, then $x=\frac 23\pi $ and $\cos(\frac{2^{k+1}}{3}\pi)=-\frac 12$ for all $k\in\mathbb N$. Hence, $\frac 1n\sum_{k=0}^n\cos(2^kx) $ converges to $-\frac 12$ and not to zero. – Jochen Jul 28 '22 at 20:43
  • Yes u are right. Thanks a lot. Corrected. Let me know if there are other problems – puppyHuazai Jul 28 '22 at 21:06