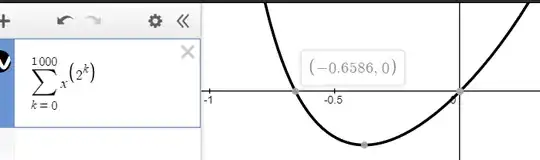
I was investiging the series $\sum_{k=0}^\infty{x^{(2^k)}}$ where $x\in\mathbb{R}$, and came up with this question:
Is there a closed form of the negative root of $\sum_{k=0}^\infty{x^{(2^k)}}=0$ ?
On Desmos, taking the first $5$ terms, and taking the first $1001$ terms, both give the negative root as $-0.6586$ to $4$ decimal places.
Here are my thoughts. According to this, "there is no solution in radicals to general polynomial equations of degree five or higher with arbitrary coefficients". So if we take the first five terms of the series, I would not expect a closed form of the negative root. But, based on my experience with power series, if we take the limit as the number of terms approaches $\infty$, I would be more inclined to believe that a closed form might exist.