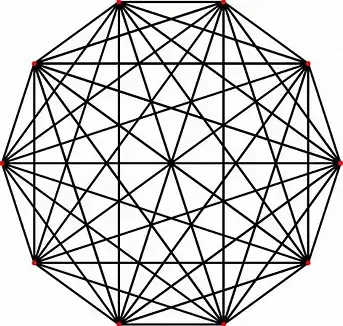
Consider a regular $n$-gon with all diagonals drawn. Here is an example with $n=10$.
What is the distribution of the areas of the regions, as $n\to\infty$ ?
That is, if we write down each region's area, how are those numbers distributed? What does the density function look like?
The number of regions is approximately $\dfrac{1}{24}n^4$ for large $n$. Here is an exact formula for the number of regions.
Context: I've been thinking about regular $n$-gons with connected vertices, and this question naturally arose.
UPDATE
I found a nice geogebra applet that allows you to play with various regular polygons with all diagonals drawn.
I would not be surprised if the answer to my question is currently unknown, because the following related question, which seems simpler than my question, is an open question: If a regular n-gon has all its diagonal drawn, does there exist a bound on the maximum number of sides of the sub-polygons thus formed (excluding the central sub-polygon when n is odd)?
UPDATE2
This question has inspired another question: Regular polygon of radius $1$ with diagonals: mysterious ring of radius $1/e$?