Wrong results when trying to check if a circle intersects with a line segment

Question

I found this answer which says how to check if a circle intersects a line segment (https://math.stackexchange.com/a/103592/565258)

After some algebra I came up with that equation

$t^2 ((x_0-x_1)^2 + (y_0 - y_1)^2) + 2t((x_0-x_1)(x_1-c_x) + (y_0-y_1)(y_1-c_y)) + (x_1-c_x)^2 + (y_1-c_y)^2 - R^2 = 0$

where $(x_0, y_0)$ and $(x_1, y_1)$ are my line segment points, $(c_x, c_y)$ is the circle center point and $R$ is the circle radius

I have that input:
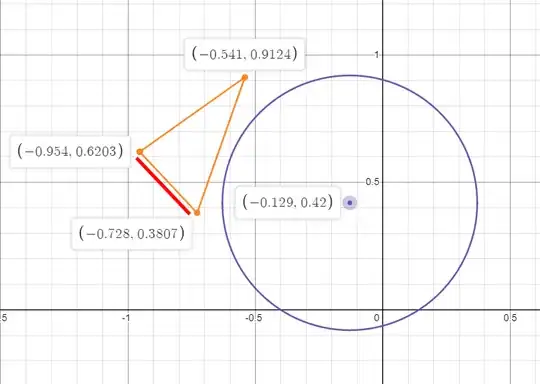
$L_1 = (-0.728324413, 0.380718231)$ -> (x0, y0)
$L_2 = (-0.953550815, 0.620288848)$ -> (x1, y1)
$C = (-0.129390717, 0.420000076)$
$R = 0.5$

Here is a graphical representation I did

Obviously there is no intersection so the $t$ in the equation must fall out of $[0; 1]$ range but actual values of $t$ I get are:
$t_0 = 0.0159721095;$
$t_1 = 0.00928559806;$

Something is wrong with my equation?

UPD
Here is the function I use for calculation. (I've hardcoded the values from the question for simplicity)

bool test()
{
    float x0 = -0.728324413f;
    float y0 = 0.380718231f;
    float x1 = -0.953550815f;
    float y1 = 0.620288848f;
    float cx = -0.129390717f;
    float cy = 0.420000076f;
    float radius = 0.5f;
    float radius_sqr = 0.5f * 0.5f;
float a = (x0 - x1) * (x0 - x1) + (y0 - y1) * (y0 - y1);
float b = (x0 - x1) * (x1 - cx) + (y0 - y1) * (y1 - cy);
float c = (x1 - cx) * (x1 - cx) + (y1 - cy) * (y1 - cy) - radius_sqr;
float d = b * b - 4.0f * a * c;

if (d >= 0.0f)
{
    float sqrt_d = sqrtf(d);

    float t1 = (-b + sqrt_d) / 2 * a;
    float t2 = (-b - sqrt_d) / 2 * a;

    if (t1 >= 0.0f && t1 <= 1.0f)
        return true;
    if (t2 >= 0.0f && t2 <= 1.0f)
        return true;
}
return false;

}

UPD #2

bool test()
{
    float x0 = 0.0993375778;
    float y0 = 0.255897522;
    float x1 = -0.294656277;
    float y1 = 0.880306243;
    float cx = -0.123999998;
    float cy = 0.414999962;
    float radius = 0.25;
    float radius_sqr = radius * radius;
float a = (x0 - x1) * (x0 - x1) + (y0 - y1) * (y0 - y1);
float b = (x0 - x1) * (x1 - cx) + (y0 - y1) * (y1 - cy);
float c = (x1 - cx) * (x1 - cx) + (y1 - cy) * (y1 - cy) - radius_sqr;
float d = b * b - 4.0f * a * c;

if (d >= 0.0f)
{
    float sqrt_d = sqrtf(d);

    float t1 = (-b + sqrt_d) / 2 * a;
    float t2 = (-b - sqrt_d) / 2 * a;

    printf("sqrt_d = %f, t1 = %f, t2 = %f\n", sqrt_d, t1, t2);

    if (t1 >= 0.0f && t1 <= 1.0f)
        return true;
    if (t2 >= 0.0f && t2 <= 1.0f)
        return true;
}

printf("d = %f\n", d);

return false;

}

result of d = -0.271311