Spivak, Ch. 12 Appendix Problem 9: Prove that slope between two points on parametric curve equal to slope of tangent to point in between two points.

Question

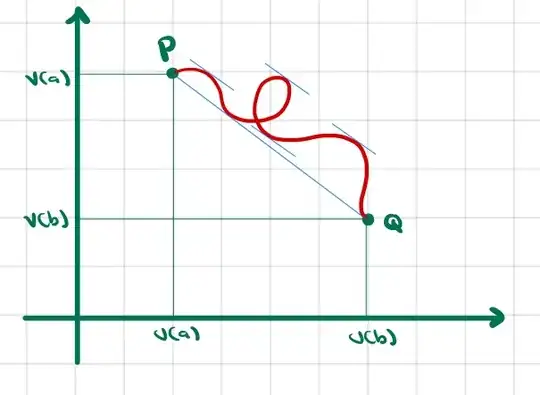
The following problem is from the appendix to chapter 12, "Parametric Representation of Curves", in Spivak's Calculus

9. Let $u$ and $v$ be continuous on $[a,b]$ and differentiable on $(a,b)$; then $u$ and $v$ give a parametric representation of a curve from $P=(u(a),v(a))$ to $Q=(u(b),v(b))$. Geometrically, it seems clear (see figure below) that at some point on the curve the tangent line is parallel to the line segment from $P$ to $Q$. Prove this analytically. Hint: This problem will give a geometric interpretation for one of the theorems in Chapter 11. You will also need to assume that we don't have $u'(x)=v'(x)=0$ for any $x \in (a,b)$.

Proof

Assuming $u(b) \neq u(a)$, the line segment from $Q$ to $P$ has a parametric representation

$$(w(t),z(t))=\left (t,v(a)+\frac{v(b)-v(a)}{u(b)-u(a)}(u(t)-u(a)) \right), t \in [a,b] \tag{1}$$

Let $d(t)=v(t)-z(t)$.

Then $d(a)=0$ and $d(b)=0$.

Since $d$ is differentiable on $(a,b)$, we can use Rolle's Theorem

$$\exists c, c \in (a,b) \land d'(c)=0$$

The derivative of $d$ at $c$ is

$$d'(c)=v'(c)-z'(c)=v'(c)-u'(c)\frac{v(b)-v(a)}{u(b)-u(a)}=0$$

$$v'(c)(u(b)-u(a))=u'(c)(v(b)-v(a))\tag{2}$$

$(2)$ looks like the result of the Cauchy Mean Value Theorem. However, the geometric interpretation hasn't come up yet I believe.

We'd like to be able to divide everything by $u'(c)$, which would give us

$$\frac{v'(c)}{u'(c)}=\frac{v(b)-v(a)}{u(b)-u(a)}\tag{3}$$

The left-hand side can be shown to be the slope of the tangent at at $(u(c),v(c))$, the right-hand side is the slope between $Q$ and $P$. Is this is the geometric interpretation of Cauchy Mean Value Theorem, namely, that given a parametric (vector-valued) function, and two points, there is some point with parameter value in between the two points' parameter values such that the slope of the parametric curve equals the slope between the two points?

But can we divide everything by $u'(c)$?

Suppose $u'(c)=0$, what does this mean? $(2)$ implies that since $u(b)\neq u(a)$ then $v'(c)=0$

My question is how do we interpret a situation in which both $u'(c)$ and $v'(c)$ are zero?

Moving on to complete the proof, if we assume $u'(c)\neq 0$ then we can divide and obtain $(3)$. But why did the problem say we'd have to assume that $v'(c)$ is also $\neq 0$?

Answer 1

Consider two assumptions:

1. there are no $x\in (a,b)$ such that $u'(x)=v'(x)=0$
2. for all $x\in (a,b)$ we have $u'(x)\neq 0$ and $v'(x)\neq 0$.

The theorem needs the assumption number 1., not 2. There can be points with $u'(x)=0$ and there can be points with $v'(x)=0$.

Without this assumption the conclusion is false. Consider the functions $u,v\colon[-1,1]\to \Bbb R$: $$u(x)=\begin{cases}0;&x<0\\x^2;&x\geq 0,\end{cases}\quad v(x)=\begin{cases}-x^2;&x< 0\\0;&x\geq 0.\end{cases}$$

If you want to prove it, you have to be aware that at some points $u'(x)=0$ and at some other points $v'(x)=0$. You can't assume that $u'(x)\neq 0$ for all $x$.

Answer 2

To evaluate $u(c) = v(c) = 0$ consider $\lim_\limits{t\to c} \frac {u'(t)}{v'(c)}$

If the denominator does not equal 0, then we can evaluate this limit directly. And if the numerator is non-zero and the denominator is zero, then the limit is undefined as is the slope of the tangent... i.e. it is vertical.

If both are zero, we have an indeterminate case. We can still evaluate the limit but we will need other tricks such as applying L'Hopital's rule.