0

Suppose that $X$ is a finite set, and that $\mathcal{P}(X)$ is the powerset of $X$. Suppose we uniformly sample two sets $A,B \in \mathcal{P}(X)$. What is the probability that $A \subseteq B$?

I ran the following simulation:

from itertools import chain, combinations
from random import sample
import matplotlib.pyplot as plt

def powerset(iterable):
    s = list(iterable)
    return chain.from_iterable(combinations(s, r) for r in range(len(s)+1))


pX = [set(i) for i in powerset(list(range(10)))]


results = []
N = 1000
for k in range(10000):
    count = 0
    for i in range(N):
        A,B = sample(pX, 2)
        if A.issubset(B):
            count += 1
        else:
            continue
    results.append(count / N)


plt.hist(results, bins=100)
plt.show()

This produces the following histogram of the estimates of this probability:

enter image description here

So the probability seems to be about 5-6 percent. Does this have an exact answer if we know the (finite) number of elements in $X$?

Asaf Karagila
  • 405,794
Galen
  • 1,946
  • 1
    I guess you can do a counting argument. Let $N=\vert X\vert$ (the cardinality of your set). There are $\binom{N}{k}$ subsets of $X$ that have cardinality $k$ (those are my $B$'s). There $2^k$ subsets of $B$. Hence, in total we get $\sum_{k=0}^N \binom{N}{k} 2^k$ admissible pairs. The number of all pairs is $2^N \cdot 2^N$. Thus, if you sample uniformly, you have the formula for your probability. Presumably there is a nicer way of writing the first sum, but as I know nothing about combinatorics, I cannot help you on that one :) – Severin Schraven May 15 '22 at 06:49
  • 1
    In fact we have $\sum_{k=0}^N \binom{N}{k} 2^k =3^N$ as shown here https://math.stackexchange.com/questions/525266/prove-sum-binomnk2k-3n-using-the-binomial-theorem – Severin Schraven May 15 '22 at 06:54
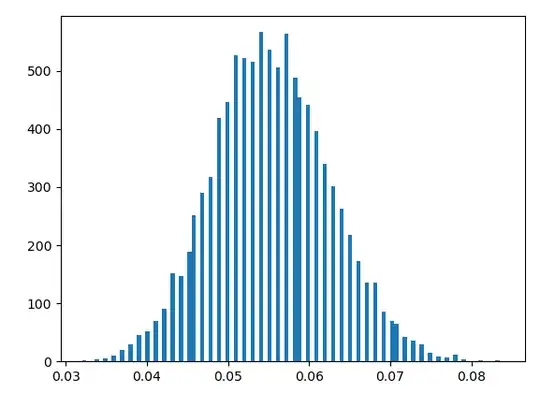
  • 3 ** 10 / (2 ** 10) ** 2 evaluates to 0.056313514709472656 in Python, so that seems about right. – Galen May 15 '22 at 06:56
  • Equivalently, (3/4) ** 10 also evaluates to 0.056313514709472656. – Galen May 15 '22 at 06:57
  • Here is a Python gist for the above. – Galen Oct 17 '22 at 01:27

3 Answers3

2

There is $1=\binom{N}{N}$ subset with $N$ elements, containing $2^N$ subsets. There are $\binom{N}{N-1}$ subsets with $N-1$ elements, each one with $2^{N-1}$ subsets, $\binom{N}{N-2}$ subsets with $N-2$ elements, each one with $2^{N-2}$ subsets, etc. So the total number of pairs $(A,B)$ where $A\subset B$ is $$ \sum_0^N\binom{N}{k}2^k=\sum_0^N\binom{N}{k}2^k\cdot 1^{N-k}=3^N $$ by the binomial formula. The total number of pairs is clearly $2^N\cdot 2^N=2^{2N}$. The final probability is thus $$ P(A\subset B)=\frac{3^N}{4^N}=\left(\frac 3{4}\right)^N $$

GReyes
  • 17,926
2

Let $N$ be the size of $X$. Choosing $A$ and $B$ with equal probability is equivalent to choosing every element $x\in X$ to be (equally probably) in $A$ or $A^c$, and independently choosing it to be (equally probably) in $B$ or $B^c$. So there are $4^N$ equally probable outcomes altogether.

Of those, $3^N$ are those outcomes where $A\subseteq B$, namely those where for each $x\in X$ we don't choose $x\in A, x\in B^c$ - but we allow for the other three possibilities.

So the total probability is $\frac{3^N}{4^N}=\left(\frac{3}{4}\right)^N$.

1

You can calculate this by hand for a few simple cases:

  • If $X$ is the empty set
  • If $X$ is a one-element set
  • If $X$ is a two-element set

In each case, write down all the choices for $A$ and $B$ and calculate how often $A\subseteq B$. Is there a pattern?

Chris Culter
  • 27,415