Can you please help me whether $N-R$ method or other methods converges?

Question

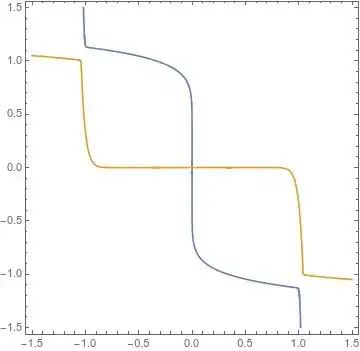
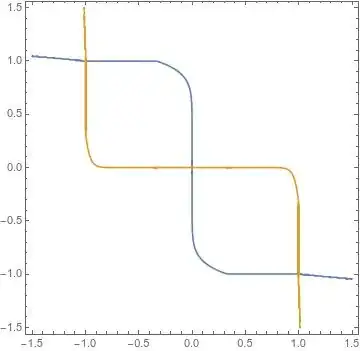
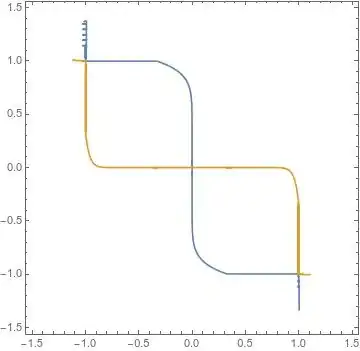
Consider the system of equations \begin{align} &f(x,y)=x+\frac{y^4}{2}+\frac{x^{32}}{4}+\frac{y^{128}}{8}=0 \\ &g(x,y)=y+\frac{x^8}{2}+\frac{y^{32}}{4}+\frac{x^{256}}{8}=0. \end{align}

I want to solve it using Newton-Raphson process or any other methods

Consider the initial guess $(x_0,y_0)=((-2)^{5/31},(-2)^{9/31})$, which is either $( 1.118,-1.223 )$ or $(x_0,y_0)=(-1.118,1.223)$.

I want to see whether the Newton-Raphson method converges with this initial guess.

Note that the initial guess $(x_0,y_0)$ is a simultaneous zero of the following truncated system obtained from the original system \begin{align} &x+\frac{y^4}{2}=0\\ &y+\frac{x^8}{2}=0. \end{align}

By hand calculation, it is laborious. For the jacobian is $$J =\begin{pmatrix} 1+8x^{31} & 2y^3+16y^{127} \\ 2x^3+32x^{255} & 1+8y^{31} \end{pmatrix} \Rightarrow J((x_0,y_0)) \approx \begin{pmatrix} 255 & -2.03 \times 10^{12} \\ 7.21 \times 10^{13} & -4104\end{pmatrix}$$ So the 2nd iteration is given by \begin{align} \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}&=\begin{pmatrix}1.118 \\ 1.223 \end{pmatrix} -J((x_0,y_0))^{-1} \begin{pmatrix}f((x_0,y_0)) \\ g((x_0,y_0)) \end{pmatrix} \end{align} which seems difficult to calculate because I can not invert the huge matrix.

The zeros of the truncated system should converge to the solutions of the original system.

Can you please help me whether N-R method or any other numerical methods converges ?

More, specifically, how to show the simultaneous zeroes of the truncated system $ x+\frac{y^4}{2}=0=y+\frac{x^8}{2}$ converges to the simultaneous zeroes of the original system $f(x,y)=0=g(x,y)$ ?

Thanks

Comments are not for extended discussion; this conversation has been moved to chat. — Pedro, May 01 '22 at 11:41

score 1 · Accepted Answer · answered Apr 28 '22 at 17:03

Here is some sage code starting the iteration in $(-1, -1)$.

IR = RealField(150)
var('x,y');
f = x + y^4/2 + x^32/4 + y^128/8
g = y + x^4/2 + y^32/4 + x^256/8
a, b = IR(-1), IR(-1)
J = matrix(2, 2, [diff(f, x), diff(f, y), diff(g, x), diff(g, y)])
v = vector(IR, 2, [IR(a), IR(b)])
for k in range(9):
    a, b = v[0], v[1]
    fv, gv = f.subs({x : a, y : b}), g.subs({x : a, y : b})
    print(f'x{k} = {a}\ny{k} = {b}')
    print(f'f(x{k}, y{k}) = {fv}\ng(x{k}, y{k}) = {gv}\n')
    v = v - J.subs({x : a, y : b}).inverse() * vector(IR, 2, [fv, gv])

The printed results are following:

x0 = -1.0000000000000000000000000000000000000000000
y0 = -1.0000000000000000000000000000000000000000000
f(x0, y0) = -0.12500000000000000000000000000000000000000000
g(x0, y0) = -0.12500000000000000000000000000000000000000000
x1 = -1.0024422735346358792184724689165186500888099
y1 = -1.0059946714031971580817051509769094138543517
f(x1, y1) = 0.048583106252741437695070286532161290853457141
g(x1, y1) = 0.035005003661522385716279832064793355617823982
x2 = -1.0020504863163137765771033606257451944731308
y2 = -1.0047357187454832971083384658776119569301797
f(x2, y2) = 0.0032718331735723517740747794193782531073714280
g(x2, y2) = 0.0013588050706032233978301227450805778637631180
x3 = -1.0020413711644051490584615403424219543507335
y3 = -1.0046329944054482289164004688385874135513553
f(x3, y3) = 0.000019403097353192714808877039288506402587269048
g(x3, y3) = 2.0763587244920856969768249854671070482986312e-6
x4 = -1.0020414289196482740462473476044443285649078
y4 = -1.0046323504589185162361046727090015558601915
f(x4, y4) = 7.5595118968724701695743900080517263081615759e-10
g(x4, y4) = 8.1922112283336376999011329830106254188700964e-11
x5 = -1.0020414289218795422093499868226092493754357
y5 = -1.0046323504338328451030885177269370761065741
f(x5, y5) = 1.1471443918740692095841154251012109118025975e-18
g(x5, y5) = 1.2374987496689888382750646154304742963132461e-19
x6 = -1.0020414289218795422127464111069351864618923
y6 = -1.0046323504338328450650188283625352002492464
f(x6, y6) = 2.6419634883773767349590310873145265485723181e-36
g(x6, y6) = 2.8548246676615458259051746549294473950928253e-37
x7 = -1.0020414289218795422127464111069351864697057
y7 = -1.0046323504338328450650188283625352001615711
f(x7, y7) = -5.6051938572992682836949183331596645251210478e-45
g(x7, y7) = 1.4538471567369977110833694426632879862032718e-44
x8 = -1.0020414289218795422127464111069351864697057
y8 = -1.0046323504338328450650188283625352001615711
f(x8, y8) = -5.6051938572992682836949183331596645251210478e-45
g(x8, y8) = 1.4538471567369977110833694426632879862032718e-44

The value $(x_7,y_7)$ is kept at the next iteration step.

I am sorry that I have edited the question adding the 4th terms $y^{128}/8$ to $f(x,y)$ and $x^{256}/8$ to $g(x,y)$. I just want to say that, indeed $f,g$ were both a nicely patterned infinite series. I decided to cut upto 3rd term of each, then added one more term. By the way, i need to understand the last part of your code. Could you please explain the last 4 lines of your code ? Finally, could i add two more terms to each $f,~g$ and work with the same code ? Thanks — MAS, Apr 29 '22 at 00:00
Thank you for your beautiful sage code. I wanted something like this. I see that the 7th iteration $(x_7,y_7)$ is a good approximate to that of my $(x_0,y_0)$ — MAS, Apr 29 '22 at 04:50
I want to replace your last line with v = v - alpha*J.subs({x : a, y : b}).inverse() * vector(IR, 2, [fv, gv]),
for some $0<alpha<1$. Can you tell how to declare the variable 'alpha' and what would be the syntax ? — MAS, May 01 '22 at 04:40
If alpha has a known value like $0.9$ just set it somewhere, maybe constants at the beginning, alpha = 0.9. Or just use it in the place it is needed with the explicit value. If it is really a variable, although i do not see the reason for doing this, just use one letter better for it, say c, and add it to the list of "variables", either together with x,y in the line that should be var('x,y,c') - or in a separate line like var('c') . Questions regarding sage can be asked here: https://ask.sagemath.org/questions/ — dan_fulea, May 02 '22 at 11:08

score 1 · Answer 2 · answered May 02 '22 at 18:36

By performing the contour plot for some truncated approximations, we can infer for which the NR algorithm will work.

$$ \cases{ x + \frac{y^9}{3}+\frac{x^{243}}{9}=0 \\ y + \frac{x^{27}}{3}+\frac{y^{243}}{9}=0 \\ } $$

Here NR works with one solution.

$$ \cases{ x + \frac{y^9}{3}+\frac{x^{243}}{9} + \frac{y^{2187}}{27}=0 \\ y + \frac{x^{27}}{3}+\frac{y^{243}}{9} + \frac{x^{6561}}{27}=0 \\ } $$

Here NR succeeds with three solutions

$$ \cases{ x + \frac{y^9}{3}+\frac{x^{243}}{9} + \frac{y^{2187}}{27}+\frac{x^{59049}}{81}=0 \\ y + \frac{x^{27}}{3}+\frac{y^{243}}{9} + \frac{x^{6561}}{27}+\frac{y^{59049}}{81}=0 \\ } $$

Here NR only gives one solution. The two contours only cross one time.

Can you please help me whether $N-R$ method or other methods converges?

2 Answers2

Linked