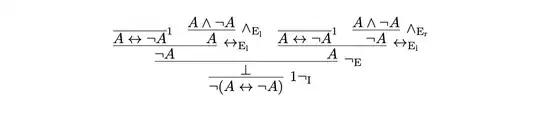My suggestion is to start first with an informal and intuitive proof, and try then to formalize it in natural deduction.
Proving that $\lnot(A \leftrightarrow \lnot A)$ amounts to show that from $A \leftrightarrow \lnot A$ a contradiction follows. So, let us suppose $A \leftrightarrow \lnot A$ and try to derive a contradiction from it.
We know that either $A$ or $\lnot A$ holds. If we assume $A$ then we get $\lnot A$ (from the hypothesis $A \leftrightarrow \lnot A$), and so we have both $A$ and $\lnot A$, absurd. Similarly, if we assume $\lnot A$ then we get $A$ (from the hypothesis $A \leftrightarrow \lnot A$), which again leads us to the same contradiction.
Therefore, it does not matter which one of the two ($A$ or $\lnot A$) holds, we always derive a contradiction from the hypothesis $A \leftrightarrow \lnot A$.
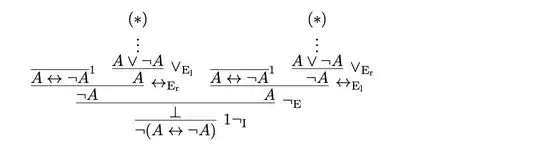
In natural deduction, the argument above can be formalized as follows ($\circ$ and $*$ mark where some assumptions have been discharged),
\begin{align}
\small
\dfrac
{
\dfrac
{{\displaystyle{\vdots}\atop\displaystyle{A\lor \lnot A}}
\ \
\dfrac
{\dfrac{[A \leftrightarrow \lnot A]^* \ \ [A]^\circ}{\lnot A}\lnot_\text{e} \ \ {\displaystyle{}\atop\displaystyle{[A]^\circ}}}{\bot}
\leftrightarrow_\text{e}
\ \
\dfrac
{\dfrac{[A \leftrightarrow \lnot A]^* \ \ [\lnot A]^\circ}{\lnot A}\lnot_\text{e} \ \ {\displaystyle{}\atop\displaystyle{[\lnot A]^\circ}}}{\bot}
\leftrightarrow_\text{e}}
{\bot}\lor_\text{e}^\circ
}
{\lnot(A \leftrightarrow \lnot A)}
\lnot_\text{i}^*
\end{align}
where ${\displaystyle{\vdots}\atop\displaystyle{A\lor \lnot A}}$ stands for a derivation of $A \lor \lnot A$ without any assumption. It is a good exercise to write such a derivation (hint: use RAA). If you get stuck, you can have a look here.
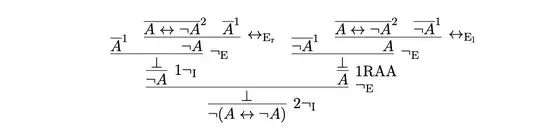
Is it necessary to use the derivation of $A \lor \lnot A$ to prove $\lnot (A \leftrightarrow \lnot A)$? Actually no. Here you can find a it (pay attention that it uses a slightly different version of the rule $\lnot_\text{e}$, but you can easily adapt it to your version of $\lnot_\text{e}$). It is closer to your initial attempts, but it does not seem very intuitive. It requires a bit of acquaintance with natural deduction.