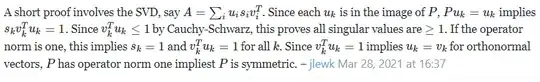Let $P$ is a projector which directly implies $P^2 = P$.
Let denote the SVD of the P as follows.
$U\Sigma V^T = P $.
The SVD results also can be represented as follows.
$P = \sum_{i} s_{i}u_{i}v_{i}^T$.
If we project a vector on the range of $P$, we will not see any difference between the original vector and the projected one. In other words, for the $u_{k}$ (note that all $u_{k}$ is in the range of $P$), we have
$$Pu_{k} = u_{k}$$
Then we also have
$$\sum_{i} s_{i}u_{i}v_{i}^Tu_{k} = u_{k}$$
Note that $s_{i}$ and $v_{i}^Tu_{k}$ are scalars, we have
$$\sum_{i} (s_{i}v_{i}^Tu_{k})u_{i} = u_{k}$$
Note that the left singular vectors are linearly independent with each other. It means that, there is a only way to make the above equation correct that selects $ s_{k}$ and $v_{k}^Tu_{k}$ such that $(s_{k}v_{k}^Tu_{k})=1$. Otherwise, we cannot make the equality as true, because $u_{k}$ cannot be represented by a linear sum of $u_{i}$s where $i\neq k$.