This is a follow-up of a recent question that I will name $(Q)$.
Reformulating question $(Q)$: being given a regular tetrahedron $(T)=(ABCD)$, how is it possible to inscribe (slanted) smaller regular tetrahedra $A'B'C'D'$ inside $(T)$ (i.e., with $A' \in BCD, B' \in ACD...$.
An elegant solution is given there (with alas few details) using an adequate rotation combined with a shrinking factor $1/3<f<1$.
This solution did not fully satisfied me because I want to know if there other means to get inscribed tetrahedra.
I have taken the vetices of the regular tetrahedron $(T)$ as the columns of this matrix:
$$T=\left(\begin{array}{rrrr}1 &-1& 1& -1\\1& 1 &-1 &-1\\1 &-1 &-1 &1\end{array}\right)\tag{1}$$
(obtained by taking a system of 4 non-neighbor vertices of a cube).
Here are the equations of the planes containing the faces of tetrahedron $(T)$:
$$\begin{cases}x+y+z+1&=&0\\-x+y+z-1&=&0\\x-y+z-1&=&0\\x+y-z-1&=&0\end{cases}\tag{2}$$
I decided to use a CAS (Computer Algebra System). After a certain number of failures, I have finaly obtained a satisfying way to get particular solutions. Here is the central part of the corresponding (Matlab CAS) program on which I am going to make some comments:
syms x1 x2 x3 x4 y1 y2 y3 y4 z1 z2 z3 z4
d12=(x1-x2)^2+(y1-y2)^2+(z1-z2)^2;
d13=(x1-x3)^2+(y1-y3)^2+(z1-z3)^2;
d14=(x1-x4)^2+(y1-y4)^2+(z1-z4)^2;
d23=(x2-x3)^2+(y2-y3)^2+(z2-z3)^2;
d24=(x2-x4)^2+(y2-y4)^2+(z2-z4)^2;
d34=(x3-x4)^2+(y3-y4)^2+(z3-z4)^2;
[X1,X2,X3,X4,Y1,Y2,Y3,Y4,Z1,Z2,Z3,Z4]=...
solve(...
x1+y1+z1+1==0,x2-y2+z2-1==0,x3-y3-z3+1==0,x4+y4-z4-1==0,...
x1+x2+x3+x4==0,y1+y2+y3+y4==0,z1+z2+z3+z4==0,...
d12==d13,d12==d14,d14==d23,d23==d24,...
z1==-1/3,...
x1,x2,x3,x4,y1,y2,y3,y4,z1,z2,z3,z4)
Let me explain the different lines following the "solve" instruction, being understood that the vertices of the looked for tetrahedra are $(x_k,y_k,z_k)$:
first line: the vertices of tetrahedra $(T')$ must belong to the faces (see (2)),
second line: the center of $(T')$ must be the origin,
third line: $(T')$ must be regular,
fourth line: one of the coordinates of the first vertex of $(T')$ is fixed arbitrarily.
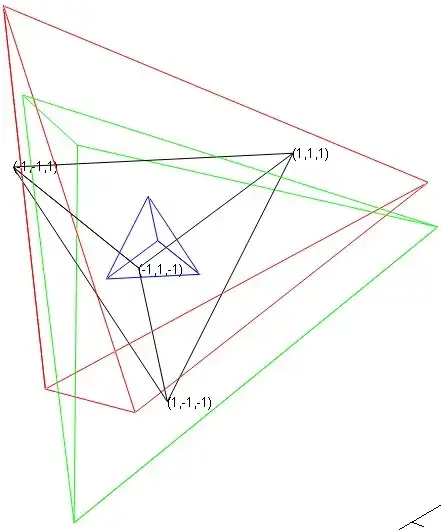
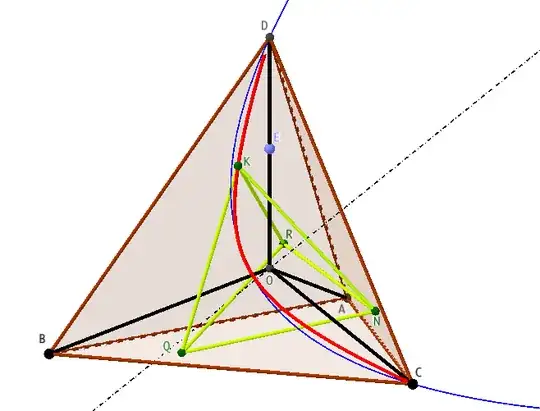
In the case at hand, we obtain almost instantly different solutions. Among them, in blue, we obtain the very particular "central" tetrahedron whose vertices are the centroids of the faces of $(T)$ (this is why we had taken the particular value $z_1=-1/3$...). The two other solutions (in red and green) are spurious, but fulfill all the conditions...
Fig. 1: Results of the program given above.
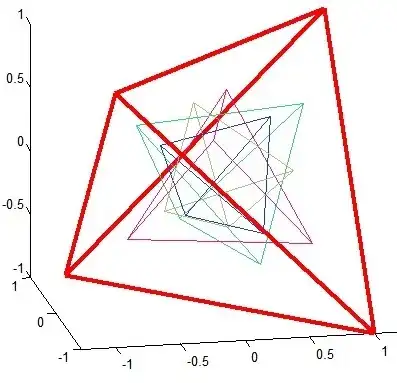
Fig. 2: With a different value of $z_1$, four different solutions for $T'$.
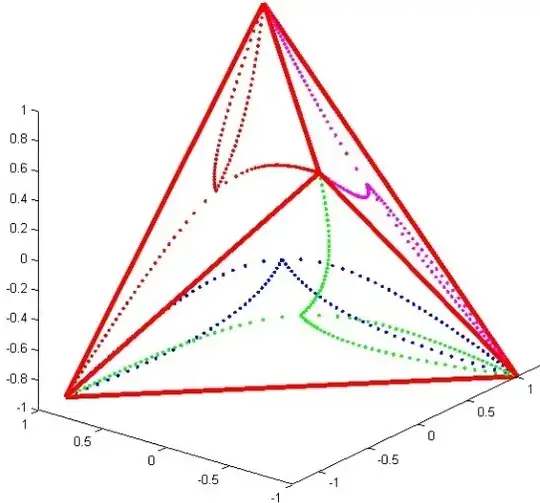
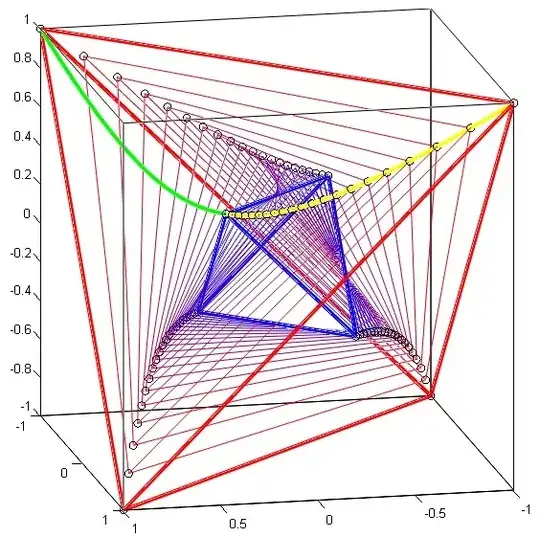
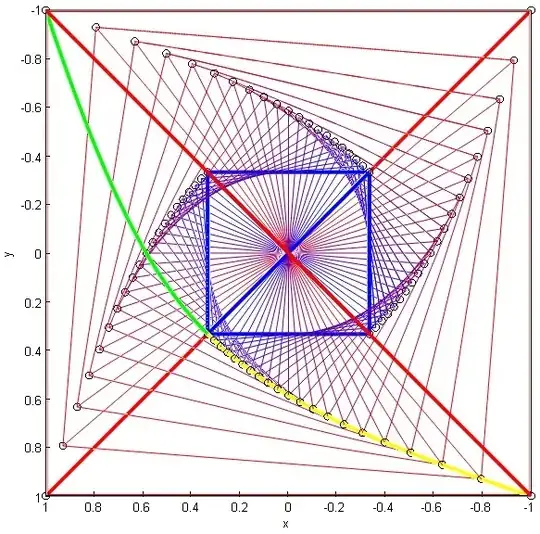
Fig. 3: The vertices of many different inscribed tetrahedra $(T')$ for many different values of $z_1$, making apparent the fact that they belong to hyperbolic arcs as shown in the answer by @Intelligenci Pauca.
Remark: when a solution $(T')$ has been found (as before, we assimilate a tetrahedron with the matrix $3 \times 4$ of the coordinates of its vertices), we can retrieve
the scaling factor $s$ by computing the ratio of norms of the columns of matrices $(T)$ and $(T')$, and
the rotation $R$ such that $T'=sRT$ by computing:
$$R=\frac1s T'T^+$$
where $T^+$ is the $4 \times 3$ pseudo-inverse of $T$.
My question is twofold:
With my method based on vertices of $(T')$, are we able to retrieve a larger set of combinations "rotation + shrinking" than in question $(Q)$ ? Are there general formulas that avoid to consider particular cases ?
Same question as in $(Q)$, to which no answer has been given: is there some interesting papers about the issue of tetrahedra inscribed in a tetrahedron ?
Edit: This question has found a new direction with the answer by Intelligenci Pauca that I have attempted to explain in a simple way (see my answer).