Moving a point on a plane

Question

I have the general equation of a plane in the form $ax+by+cz+d=0$. I also have it's normal and the coordinates of a point that lies on the plane ($E$). I want to calculate the coordinates of a new point on this plane ($F$) which lies on the circumference of a circle with its origin in $E$ at radius $r$, angle $α$.

Image representation:

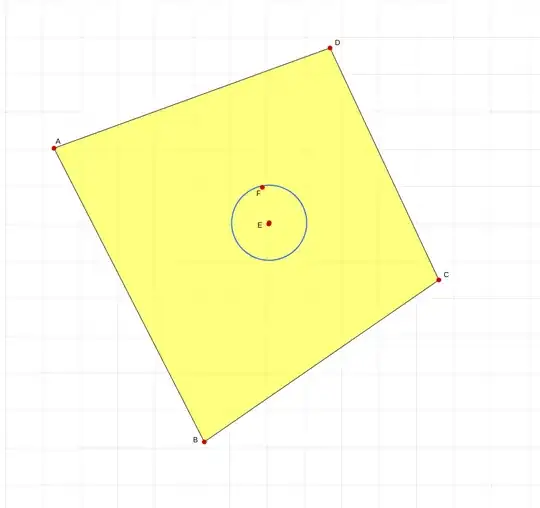
I know of the formula for calculating a point on the circumference of a circle

$$x = cx + r \cos(a)$$ $$y = cy + r \sin(a)$$

but not sure how that can be adapted for a particular plane instead of the standard XYZ axis.

Answer 1

One way to parameterize this circle is as follows. Let $n$ denote a normal vector to the plane (for instance, $n = (a,b,c)$).

1. Find a non-zero vector $v = (v_x,v_y,v_z)$ parallel to the plane (i.e. perpendicular to the plane's normal vector). Let $\hat v$ denote the normalized vector $\hat v = \frac{v}{\|v\|}$.
2. Compute the cross-product $w = n \times v$. $w = (w_x,w_y,w_z)$ is a vector in the plane that is orthogonal to $v$. Let $\hat w$ denote the normalized vector $\hat w = \frac w{\|w\|}$.
3. The circle of radius $r$, within the given plane, centered at point $E:(x_0,y_0,z_0)$ can be parameterized with the following equation: $$ (x,y,z) = (x_0,y_0,z_0) + r\cos \alpha( \hat v_x,\hat v_y,\hat v_z) + r\sin \alpha(\hat w_x,\hat w_y,\hat w_z). $$

$\alpha$ denotes the angle within the plane between the vectors $v$ and $\vec{EF}$.