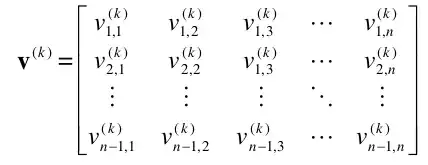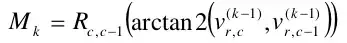3

I have been looking into the generalisation of rotation about an axis in 3D. Which I have found to be is rotation of a vector in N dimensional space about an N-2 dimesnional subspace. The paper General n-Dimensional Rotations introduces a very interesting algorithm to compute such a matrix and do such transformation. But during the change of basis(the initial rotations in order to embed the N-2 subspace into $X_1 X_2 X_3 ... X_{N-2}$) they use the coordinates of the points that are produced after the applications of each rotation matrix.

A matrix is formed which contains the coordinates of all the (N-1) elements.

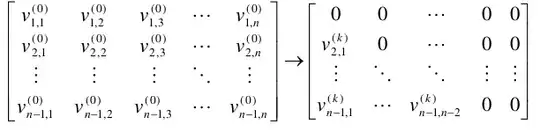
enter image description here

The change of basis here makes the columns of the last two elements equal to zero due to which the said matrix can be embedded in N-2 dimensional space. The transformation can be written as

enter image description here

For making the $v^{k}_{r,c}$ equal to 0 we use the matrix given by

enter image description here

Now as you can observe the rotation matrix takes in as input $v^{k-1}_{r,c}$ which is the coordinates after the application of the last rotation matrix. This procedure is repeated until most of the coordinates of the starting plane(the plane we wanted to do rotation about) is zero and then we apply the rotation about this plane. And finally we apply the inverse of the basis change.

My Question - Is there any method in which we do not have to check the coordinates obtained at the intermediate steps, rather we can at the beginning look at the coordinates of the plane and decide the input to all the rotation matrices, to do the basis change and finally the rotation about the subspace.

Perhaps this is somehow possible by using spherical coordinates, I have been trying but not able to find any such method.

Parmeet Singh
  • 81
  • Welcome to Math.SE! This is an interesting question, but I am having some difficulty following what specifically the problem is - e.g. could you use MathJax to include some of the specific equations/steps of the algorithm from the paper in your question? E.g. what do you mean by "check the coordinates obtained at the intermediate steps", what part of the algorithm amounts to "checking coordinates". – hasManyStupidQuestions Dec 26 '21 at 15:38
  • 1
    Hi I modified my question hopefully this will be more understandable now – Parmeet Singh Dec 26 '21 at 18:03
  • 1
    Proferring an old question I answered for comparison. The recipe I use is to write that $(n-2)$-dimensional subspace as an intersection of two hyperplanes, and the make the composition of the two reflections determined by those two hyperplanes. The angle of rotation is twice the angle between the chosen two hyperplanes. – Jyrki Lahtonen Dec 26 '21 at 18:35
  • @JyrkiLahtonen thanks for your answer. But I am not sure if this answers my question. You have described a recipe of how to obtain the rotation matrices but I was rather looking for how would one use such rotation matrices to get some points into the said subspace, before rotation about this subspace. – Parmeet Singh Dec 27 '21 at 06:18

0 Answers0