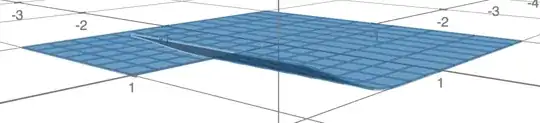
Let $\Omega =\left(-1,1 \right)^2\setminus\left( \left[0,1 \right)\times \{ 0\}\right)$
and $u(x_1,x_2)=\hat u(x_1)$ for $x_1,x_2 >0$ and $u(x_1,x_2)=0$ else.
I am looking for a function $\hat u$ such that $u \in W^{1,\infty}(\Omega)$ and $u$ is not Lipschitz continous on $\Omega$.
I have failed to come up with a suitable function $\hat u$. Any hints what I may try ?
Would appreciate any help.