I think the answer is yes, but I'm having trouble proving it. My attempt was to prove the converse instead, so first assume theres a discontinuity at $x_0$ and then show this means the graph is not path connected somehow with some path starting at $x_0$. But I can't figure anything with this approach.
Asked
Active
Viewed 163 times
1
-
1But this function is not continuous at 0, since its not even defined at 0? The graph is also not path connected so I don't think this proves anything? – nabu1227 Jan 20 '22 at 02:59
-
I completely misremembered the definition of a graph. Sorry! – Calvin Khor Jan 20 '22 at 04:17
-
1Similar (if not duplicates): https://math.stackexchange.com/q/1243983/42969, https://math.stackexchange.com/q/2968327/42969, https://math.stackexchange.com/q/2928893/42969 – Martin R Jan 20 '22 at 05:40
2 Answers
8
What about a function $f:\Bbb{R}^2\to \Bbb{R}$ whose graph in $\Bbb{R}^3$ looks like this?
Pardon the bad picture, but it's meant to be a plane with a little ramp sticking off. The idea is that this is path connected because you can drive up the ramp, but the associated function (which you can imagine how to define) is not continuous.
Alekos Robotis
- 27,579
-
(+1) There's a plot I made for a different question here that also does the job, if you want you can probably edit the math3d.org plot to make it more like yours – Calvin Khor Jan 20 '22 at 03:38
-
I was able to draw a better picture on my tablet. I just didn't have it at the time. Hopefully this is clear enough now. – Alekos Robotis Jan 20 '22 at 05:25
-
It was plenty clear to me to begin with :) but it is a nice improvement – Calvin Khor Jan 20 '22 at 05:26
4
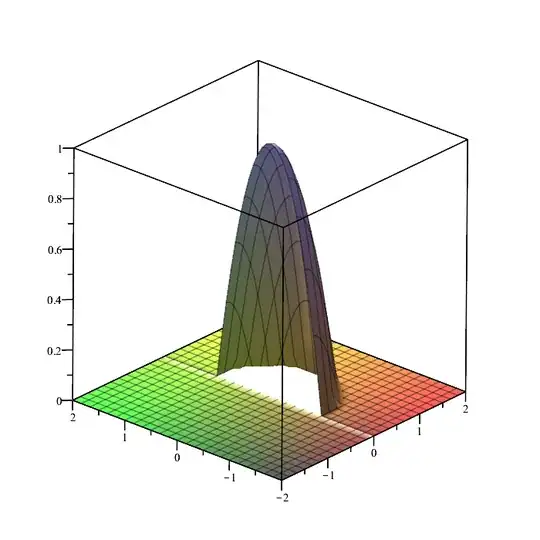
(Probably for $n = 1$ the claim it is true, but) for general $n$ it is not.
Consider the example $n = 2, m = 1$,
$$f(x, y) = \left\{\begin{array}{cl}0, & x<0 \\ \operatorname{max}(0, 1 - (x^2 + y^2), & x \geq 0 \end{array}\right. .$$
Travis Willse
- 108,056