I need to calculate the angle of the front steering wheel using a collapsible piston(linear sensor). 'x' is used to represent the length in inches of the movable part of the sensor and is the independent variable.
θ represents the steering angle. The angle is 0 when the wheels are perfectly straight and increases as the wheels turn to the left and decreases as the wheels turn to the right.
This is the image where the θ is zero:
This is when it's steering all the way to the left:
and this is when it's steering all the way to the right:
I'm trying to solve it using the parametric equations of the circle; Relating the piston with the equations using the euclidean distance. As it turns out, I'm having a hard time solving for theta.
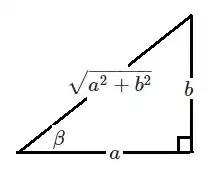
In the following two images you can see my derivations:
I'm stuck here:
$$b\cdot cos(\theta) - a\cdot sin(\theta) = \frac{a^2 + b^2 - d^2 + r^2}{2\cdot r}$$
Any help would me appreciate it!
theta-functionstag, which refers to something else: https://en.wikipedia.org/wiki/Theta_function – Travis Willse May 29 '20 at 07:11