I've been reading up on Bayes Theorem and thought I'd try to apply it to a hypothetical medical test, but I'm not sure I'm applying it correctly.
I contrived this scenario:
- A medical test has a sensitivity of 60%. In other words, the false negative rate is 40%.
- The test also has a specificity of 90%.
- The prevalence of the particular disease in the population is 5%.
- I have no symptoms of the disease, but I take the test anyway and get a negative result.
- I want to know the probability that I received a false negative.
I was thinking this could be calculated as
$$ P(\text{False Negative Result}) = P(\text{Disease|Negative}) = \frac{P(\text{Negative|Disease})\cdot P(\text{Disease})}{P(\text{Negative})} = \frac{(1-\text{Sensitivity})\cdot P(\text{Disease})}{P(\text{Negative})}$$
So in this example...
$$ P(\text{False Negative Result}) = \frac{(1-0.60)(0.05)}{((1-0.60)(0.05) + (0.90)(1-0.05))} = 0.02 $$
But I'm not sure if I'm missing something?
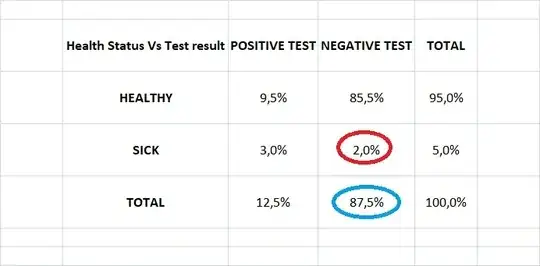
P(False Negative Result)differs from theNegative Predictive Value. I'll have to do some more research on this. Would it be correct to assume the Negative Predictive Value is associated with a test, but the P(False Negative Result) is associated with an event? – CodeLearner140 Nov 29 '21 at 06:25