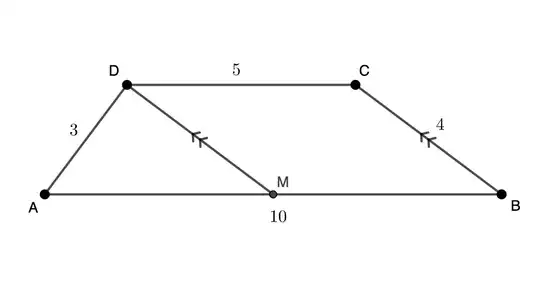
I was going through some Olympiad Maths and found this question:
Given a trapezoid with its upper base $5$ cm long, lower base $10$ cm long, and its legs are $3$ and $4$ cm long. What is the area of this trapezoid?
Yeah, I know. There are equations to calculate this, I found some equations on Math Stack Exchange too.
What I don’t understand is that this is an Olympiad question. The proofs that I saw to create the formulae did not look like something that should appear in an Olympiad question. Am I missing something, or do I actually need to create my own formula to solve this question? Keep in mind that this is a timed test; if I was actually taking this test, I would have to solve this in 2 minutes maximum.