26

If all sides: $a, b, c, d$ are known, is there a formula that can calculate the area of a trapezoid?

I know this formula for calculating the area of a trapezoid from its two bases and its height:

$$S=\frac {a+b}{2}×h$$

And I know a well-known formula for finding the area of a triangle, called Heron's formula:

$$S=\sqrt {p(p-a)(p-b)(p-c)}$$

$$p=\frac{a+b+c}{2}$$

But I could not a formula for finding the area of a trapezoid in the books.

Community
  • 1
Newuser
  • 576
  • 3
    What do you mean by "trapezoid"? In North America, it's a quadrilateral with at least one pair of parallel sides; elsewhere, it's a quadrilateral with no parallel sides. – David Richerby Feb 06 '18 at 22:27

11 Answers11

38

This problem is more subtle than some of the other answers here let on. A great deal hinges on whether "trapezoid" is defined inclusively (i.e. as a quadrilateral with at least one pair of parallel sides) or exclusively (i.e. as a quadrilateral with exactly one pair of parallel sides). The former definition is widely considered more mathematically sophisticated, but the latter definition is more traditional, is still extensively used in K-12 education in the United States, and has some advantages.

As the other responses have pointed out, if one defines "trapezoid" inclusively, then any parallelogram is automatically a trapezoid, and as the side-lengths of a parallelogram do not determine its area, it is not possible (even conceptually) that there could be a formula for the area of a trapezoid in terms of its side lengths.

However, if "trapezoid" is defined exclusively, then things are quite different. Consider a trapezoid with parallel bases of length $a$ and $b$ with $b>a$. Let $\theta$ and $\phi$ respectively denote the angles formed by the legs $c$ and $d$ with the base $b$. Then we have the following relationships: $$c\cos\theta + d\cos\phi = b-a$$ $$c\sin\theta = d\sin\phi$$ These conditions uniquely determine $\theta$ and $\phi$, and therefore among non-parallelogram trapezoids, choosing the lengths of the parallel sides and the lengths of the bases uniquely determines the figure. In particular we would have $$\cos\theta = \frac{(b-a)^2+c^2-d^2}{2c(b-a)}$$.

The height of the trapezoid would then be $h=c\sin\theta$ (or if you prefer $h=d\sin\phi$, which is equal to it), so the area of the trapezoid can (in principal) be computed. If you really want to carry it out, you would have

$$\sin\theta = \sqrt{1-\left( \frac{(b-a)^2+c^2-d^2}{2c(b-a)} \right)^2}$$ so the area would be $$A=\frac{a+b}{2}c\sqrt{1-\left( \frac{(b-a)^2+c^2-d^2}{2c(b-a)} \right)^2}$$ I am not sure if there is a simpler expression, however.

mweiss
  • 24,547
  • 2
    You're right. I was thinking this through in response to your comment. One way to see it geometrically rather than algebraically is to imagine the two parallel edges joined at one pair of ends by a third edge. As you rotate that edge around a semicircle, changing the angles it makes with the parallel sides, the distance between the other ends of the parallel edges varies continuously with no repeat values. – Ethan Bolker Feb 05 '18 at 22:12
  • 1
    This is the address: http://www.1728.org/quadtrap.htm – Seyed Feb 05 '18 at 22:22
  • 9
    On the other hand, the question does not even specify which two of the four lengths correspond to the pair of parallel sides. If you are only given four lengths, do they determine a unique trapezoid? –  Feb 06 '18 at 06:41
  • 3
    @Rahul For some "lucky" values of the four length, you can deduce which two are parallel, and there is a unique area. But in general, there is more than one way of choosing the parallel sides. Given lengths $1,2,2,4$, you can either take $4$ and $1$ as the parallel sides, or you can take $4$ and $2$ as the parallel sides. This leads to different trapezoids with different areas ($\frac54 \sqrt{7}$ and $\frac34 \sqrt{15}$, respectively, if I do it correctly). – Jeppe Stig Nielsen Feb 06 '18 at 15:48
  • @Rahul no -- for this formula it's important to know in advance which two sides are parallel, and call them a and b, and the others c and d. If you flop them around, you can get a different answer, corresponding to a different trapezoid with the same four side lengths (but a different shape). – hobbs Feb 06 '18 at 18:28
  • 3
    "A great deal hinges on whether 'trapezoid' is defined inclusively (i.e. as a quadrilateral with at least one pair of parallel sides) or exclusively (i.e. as a quadrilateral with exactly one pair of parallel sides)." Stuff hinges on more than that! Outside North America, a trapezoid is a quadrilateral with no parallel sides (at least one pair would be a "trapezium" in that nomenclature). – David Richerby Feb 06 '18 at 22:29
  • If you define "trapezoid" inclusively (so that a parallelogram is a trapezoid) then, in the case of a parallelogram, you'll have θ + ϕ = 180 degrees. So that your equations become: – Claudio Buffara Feb 27 '18 at 01:10
  • I've answered with a slight modification to your answer. – AmbretteOrrisey Nov 23 '18 at 08:04
17

To add a derivation that puts the square root factor in a Heronian context ...

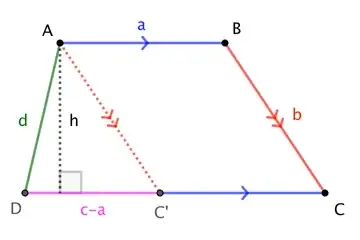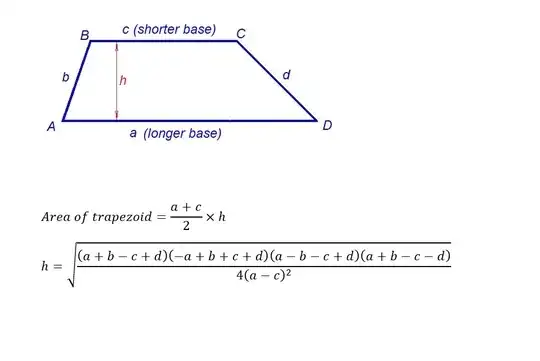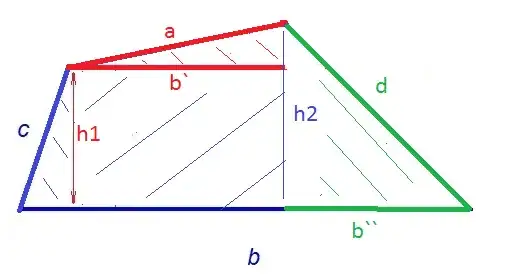
enter image description here

For $c := |\overline{CD}| \neq |\overline{AB}| =: a$, $$|\square ABCD| = \frac12 (a+c) \cdot h = \frac12 (a+c) \cdot \frac{2 |\triangle AC^\prime D|}{|\overline{C^\prime D}|} = \frac{a+c}{|a-c|}\;|\triangle AC^\prime D|$$

Then, applying Heron's Formula to a triangle with side-lengths $b$, $d$, $c-a$, we have $$|\triangle AC^\prime D| = \frac14\sqrt{((c-a)+b+d)(-(c-a)+b+d)((c-a)-b+d)((c-a)+b-d)\;}$$

Blue
  • 83,939
8

A note for the case when only two sides are parallel, just the set of four side lengths do not determine the area. An additional information is needed to define, which pair of sides are parallel. An illustrative example for side lengths $19,23,29,31$:

enter image description here

g.kov
  • 13,841
  • Yeah, I was just writing a comment to mweiss's answer about the same thing. – Jeppe Stig Nielsen Feb 06 '18 at 15:53
  • I was expecting a slightly different diagram, like your first in terms of which sides have which length, but with $29$ parallel to $31$ instead of $19$ parallel to $23$ – Henry Feb 07 '18 at 12:35
  • 1
    @Henry: Well, have you tried to construct it with side of length 29 parallel to side of length 31 with the other two 19, 23? – g.kov Feb 07 '18 at 13:33
  • @g.kov - good point, as in effect I would need to construct a $19,23,2$ triangle. So does this suggest that given the order of the sides and them all being different, there would only be one possibility (and its reflection) for a pair of parallel sides, and so only one area? – Henry Feb 07 '18 at 15:05
  • @Henry: This is probably an interesting new question. – g.kov Feb 07 '18 at 15:17
6

This is how to calculate the area of a trapezoid when the four sides are known: enter image description here

Seyed
  • 9,041
6

Hint (if we know the parallel sides):

enter image description here

From The picture:

take: $a=AB, b=BC, c=CD, d=DA,x=AE$

so we have: $ h=ED=\sqrt{d^2-x^2}=\sqrt{b^2-(a-c-x)^2}=CF $

solve for $x$ and find $h=\sqrt{d^2-x^2}$

Find the area $A=\frac {a+b}{2}h$

Emilio Novati
  • 64,377
4

There can't be such a formula. The side lengths do not determine the area.

Think about all the rhombi with four sides of length $1$. They are all trapezoids (even parallelograms) with the same side lengths but different areas, which can be anything between $0$ and $1$.

Ethan Bolker
  • 103,433
  • I dont understood.How? – Newuser Feb 05 '18 at 21:54
  • 3
    If "trapezoid" is defined exclusively (i.e. as a quadrilateral with exactly one pair of parallel sides, so that parallelograms are not trapezoids) then do the side lengths determine the figure? – mweiss Feb 05 '18 at 21:55
  • @mweiss You're right. See my comment on your answer. – Ethan Bolker Feb 05 '18 at 22:14
  • 1
    if these conditions are met $a+c+d > b$ , $a+c < b$ , $a+d < b$ , there should be a unique trapzoid in universe with these parameters. and of course with a calculable area. – Abr001am Feb 06 '18 at 16:08
3

I derived the formula for the area using the same procedure as is used to show Heron's Formula. Looking at the end formula, I realized that the formula follows quite simply from Heron's Formula.

Given a trapezoid with unequal parallel bases $a$ and $b$,

enter image description here

consider the triangle with base $|b-a|$ and sides $c$ and $d$:

enter image description here

Using $s=\frac{|b-a|+c+d}2$, the area of the triangle is $$ \text{Area of Triangle}=\sqrt{s(s-c)(s-d)(s-|b-a|)} $$ The altitude of the trapezoid and the triangle are the same, so the area is proportional to the average of the lengths of the bases. That is, $$ \bbox[5px,border:2px solid #C0A000]{\text{Area of Trapezoid}=\frac{b+a}{|b-a|}\sqrt{s(s-c)(s-d)(s-|b-a|)}} $$

robjohn
  • 353,833
  • I get it now. I had some difficulty at first ... but then I visualised it as two seperate triangles made by drawing a diagonal across the trapezium: one with a as base (or lid, rather) & the other with b as base: the former has area a/|b-a| × that of your Heron triange - the latter b/|b-a| × it; so the sum of them, the area of the trapezium, is (b+a)/|b-a| × it! Neat! – AmbretteOrrisey Nov 23 '18 at 21:34
2

enter image description here

-For the trapzoid abcd to have parallel sides it requires all these conditions to be set for uniqueness of area:

  • $a+b+c>d$, $b+a<d$, $c+a<d$.

-Neverthless, a trapzoid with non parallel sides can not be defined just by his side lengths, but a fifth coordinate added should.

In this experience we show how come multiple trapzoid shapes can be formed with same lengths of edges.

Imagine we bring a fork and a knife to start dining on some digestable geometrical concepts :

enter image description here

A thread and two pins:

enter image description here

We instill the pins on some flat table:

enter image description here

Then take the fork and the knife, choose two fixed points in the string, then pull it from these points with those tools without changing the fulcrum points.

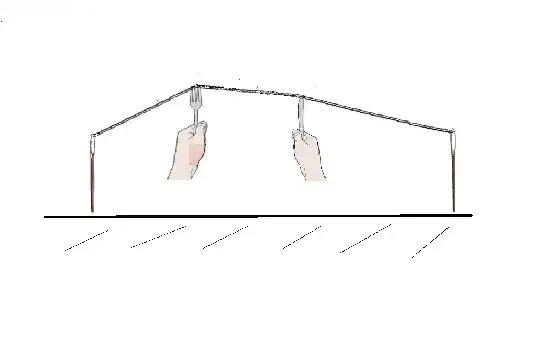
enter image description here

Distance of the chord from the pinpoints to the coordinates of fulcrums dosn't change, while the shape of the trapzoid changes infinitely!

now envisage that $h_1$ is figured by the fork, $h_2$ symbolised by the knife, h1 is directly relative to h2 always regarding the same side lengths. We will show in the following trigonometric relations:

  • $\cos\theta=b`/a$,
    $sin\theta=(h_2-h_1)/a \implies \sqrt{1-(b`/a)^2}=(h_2-h_1)/a$
  • $b``/d= \sqrt{1-(h_2/d)^2}$
  • $(b-b`-b``)/c= \sqrt{1-(h_1/c)^2}$

Since there is 4 unknowns $b`,b``,h_1,h_2$ we can formulate $h_1$ in function of $h_2$ and 4 side constants.

Credits for the images goes to canstockphoto.com

Abr001am
  • 766
1

I think you mean Brahmagupta's formula, not Heron's formula. There is no formula for the area of trapezoid given the lengths of the sides, because the sides alone do not determine the area. This is true even for a parallelogram. Imagine a parallelogram made of four sticks, joined together by pins at the corners. Then you can slide it closed by moved the top side parallel to the bottom side. You'll get zero area when the top and bottom coincide, and maximum are when you have a rectangle.

In the case of Brahmagupta's formula, the quadrilateral is circumscribable, and you can't change the sides like that.

saulspatz
  • 53,824
  • 2
    "This is true even for a parallelogram" - in fact, as other answers show, it is true only for a parallelogram. For a trapezium which is not a parallelogram the size lengths do determine the area (provided you are told which are the lengths of the parallel sides). – Martin Bonner supports Monica Feb 06 '18 at 12:55
  • @MartinBonner True, but I've never heard the definition of a trapezoid that excludes a parallelogram. – saulspatz Feb 06 '18 at 14:31
  • @saulspatz In the United States, at least, that is the norm at the pre-college level, and has been for more than a century. See my answer on MESE at https://matheducators.stackexchange.com/a/13766/29 for a historical survey. – mweiss Nov 27 '18 at 01:29
1

It depends on your definition of trapezoid. If it includes parallelograms, then No: here are two trapezoids, same side-lengths, different area:

enter image description here

Community
  • 1
M. Winter
  • 30,828
1

M Weiss put

$$A=\frac{a+b}{2}c\sqrt{1-\left( \frac{(b-a)^2+c^2-d^2}{2c(b-a)} \right)^2} .$$

I would rather have that answer symmetrical in $c$ & $d$, which would be

$$A=\frac{a+b}{4(b-a)}\sqrt{(b-a)^4+2(b-a)^2(c^2+d^2)+(c^2-d^2)^2} .$$

But it's just that to my taste it looks odd that it's not symmetrical in $c$ & $d$ ... my mind just protests that it ought to be!

Or

$$A=\frac{a+b}{4(b-a)}\sqrt{(b-a)^2((b-a)^2+2(c^2+d^2))+(c^2-d^2)^2} ,$$

even.

AmbretteOrrisey
  • 1,001
  • 6
  • 12