Short question: Let $ r,t,h\ge0 $ and $ G_1,G_2 $ be i.i.d. standard Gaussians. Is it true that $$ \Pr[\{(r+G_1)^2\le t\}\cup\{(r+G_1)^2+G_2^2\le h\}]\le\Pr[\{G_2^2\le t\}\cup\{(r+G_1)^2+G_2^2\le h\}]. $$
Motivation:
I formulated the inequality in such a way since there is nice geometry behind it.
In the following figure, $\mathcal{D}_0$ denotes the green disk and $\mathcal{D}_1,\mathcal{D}_2$ denote the vertical and horizontal (infinite) bands with the disk clipped out, respectively.
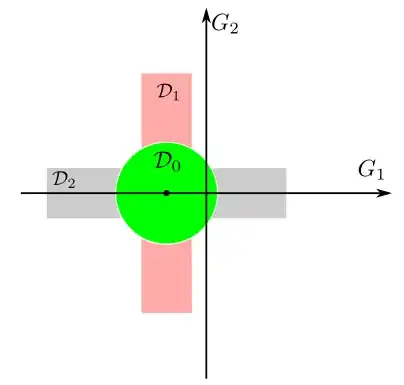
Then the LHS of the inequality is the probability that $(G_1,G_2)$ falls into the region $\mathcal{D}_1\sqcup\mathcal{D}_0$, and the RHS is the probability that $(G_1,G_2)$ falls into the region $\mathcal{D}_2\sqcup\mathcal{D}_0$. The inequality is nontrivial only when $r>0$ and $t>0$. It's clearly true when $t\ge h$ since the disk is contained in the bands. According to numerics, I believe it's true for any $r,t,h\ge0$. However, I could not prove it. Any help is much appreciated.
Disclaimer: This is not a HW question. It arises in a research project on high-dimensional statistics.