7

The working-out of this question has really confused me. I know the basics of probability but I don't get the calculations here. I think 13C2 * 4C2 determines the number of possible pairs, and the stuff in the brackets is the number of combinations possible with the cards remaining after a pair is obtained—but, in them, what does does each number specifically do?

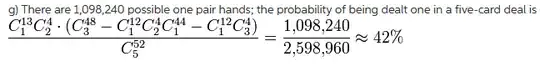The working-out I'm referring to.

Thanks in advance.

Rodrigo de Azevedo
  • 23,223
EH86055
  • 81
  • 6
    It's complicated because you don't want the other three cards to give you another pair or a three-of-a-kind (making the hand a full house). Those are exactly the two cases being subtracted here. – Jaap Scherphuis Oct 25 '21 at 11:00
  • @JaapScherphuis If the given pair is extended to three of a kind with the other three cards , the result need not be a full-houese. Is this considered in the above formula ? – Peter Oct 25 '21 at 11:05
  • 2
    @Peter The first term in the brackets is all possible three card sets that do not have any card matching the pair you already have, so extending the existing pair is already excluded. It is only the addition of an extra pair or triple that remains to be subtracted. That said, Tommik's answer is a much easier way to count all the valid possibilities of three additional cards. – Jaap Scherphuis Oct 25 '21 at 11:09
  • @JaapScherphuis OK, I got it. Thank you. – Peter Oct 25 '21 at 11:10

1 Answers1

15

A simpler and equivalent way is the following:

The number of favourable events are:

$$13\times\binom{4}{2}\times\binom{12}{3}\times 4^3=1{,}098{,}240$$

this because:

  • you have 13 different ways to choose the pair

  • you have $\binom{4}{2}$ different suits for your chosen pair

  • you have $\binom{12}{3}$ different ways to choose the 3 remaining cards

  • you have $4^3$ different suits for the 3 remaining cards

tommik
  • 33,201
  • 4
  • 17
  • 35