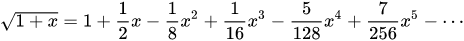Square root of an invertible complex matrix

Question

Let $A$ be an invertible $n\times n$ complex matrix. Does there always exists an invertible complex matrix $B$ such that $A = B^2$ ?

My attempt : Consider the Jordan form of $A$, say $$J= \begin{pmatrix} \lambda_1 & 1 & \cdots \\ 0 & \lambda_2 & \cdots \\ \vdots & \vdots & \cdots \end{pmatrix} $$ with $A = Q^{-1}JQ$ for some $Q$ and $\lambda_i \neq 0 $ for all $i$ since $0\neq\operatorname{det}(A) = \operatorname{det}(J) = \Pi_{i=1}^n \lambda_i$. But I don't know how to construct such $B$ from this form.

just notice that the Jordan form of the square of any invertible matrix in Jordan form is itself (with different eigenvalues) — Exodd, Sep 29 '21 at 13:42
Does this answer your question? When does a complex matrix have a square root? — Brauer Suzuki, Sep 29 '21 at 15:05

score -1 · Answer 1 · answered Sep 29 '21 at 17:34

-1

Use a binomial expansion if $A$ is "close" to the identity: $$ A^{1/2}=(I+(A-I))^{1/2}=... $$ From Wikipedia

answered Sep 29 '21 at 17:34

Disintegrating By Parts

91,908
6
76
168

Square root of an invertible complex matrix

1 Answers1