2

The following picture

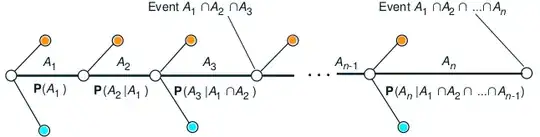
probability tree

should be an intuitive diagram for the well-known formula $$ P(A_1 \cap \cdots \cap A_n) = P(A_1) P(A_2 \mid A_1) P(A_3 \mid A_1 \cap A_2) \cdots P(A_n \mid A_1 \cap \cdots \cap A_{n-1}). $$

I would like to know what the orange and cyan dots represent. The central row is quite clear. For the upper row, I believe that the orange dots can easily be assumed as the $A_i$'s. What about the cyan dots?

ryang
  • 44,428
lkgdort
  • 21
  • 1
  • 1
    As the image is taken from its context, we can only guess what that means, it depends on the context. However, I think the cyan and orange dots just symbolize that there may be more branches of the tree and the line is the main branch you're currently looking at. I don't think it represents the $A_i$, as they're the events in the main branch – LegNaiB Sep 15 '21 at 15:37
  • @LegNaiB I think events on the main branch are the intersections, as pointed out in the picture. – lkgdort Sep 16 '21 at 05:29

1 Answers1

1

The given diagram is just an excerpt of a probability tree that represents a probability experiment with $n$ trials.

Each column represents a trial, each circle represents a conditional trial outcome, and each branch (between adjoining circles) represents the corresponding conditional event; e.g., the branch leading to the third (not counting the originating leftmost one) white circle represents the event $(A_3|A_1A_2)$ of outcome $A$ in the third trial given outcomes $A$ in the preceding trials.

Each path represents an elementary event (i.e., an event containing a particular experiment outcome); e.g., the horizontal path connecting all the white circles represent the event $A_1A_2\ldots A_n$ of the experiment having outcome A in all its trials. The experiment's elementary events collectively comprise its sample space. (Note that an event is simply a subset of the sample space.)

OP: I would like to know what the orange and cyan dots represent. The central row is quite clear. For the upper row, I believe that the orange dots can easily be assumed as the $A_i$'s. What about the cyan dots?

In the third column, the orange circle might represent the conditional trial outcome $(B_3|A_1A_2),$ i.e., the outcome $B$ in the third trial given outcomes $A$ in the preceding trials; while the cyan circle might represent the conditional trial outcome $(C_3|A_1A_2).$

Now, to be clear: the event or trial outcome $A_7$ is the event of outcome $A$ in the seventh trial regardless of the outcomes in the other trials; thus it includes—though isn't limited to—the experiment outcome $B_1B_2\ldots A_7C_8\dots C_n;$ therefore, it isn't being represented by any orange dot.

ryang
  • 44,428