A question related to skew symmetric matrix and Orthogonal matrices

Question

Consider the following problem asked in a masters exam for which I am self studying.

Write V for the space of $3 \times 3$ skew - symmetric real matrices.

(A) Show that for $A\in SO_3(\mathbb{R})$ and $M\in V$ , $AMA^t \in V$.

(B) Show that there does not exists $M \in V$ , $M \neq 0$ such that for every $A\in SO_3(\mathbb{R})$ , A . M belongs to span of M.

(Note that $SO_3(\mathbb{R})$ is a subgroup of $GL_3 (\mathbb{R})$ such that any element $x\in SO_3(\mathbb{R})$ consists of all orthogonal matrices with Determinant =1).

I have done (A) part, but I am struck on (B). I thought I should assume that let there exists such a matrix $M \in V$ but I am unable to think of any contradiction.

So, Can you please outline a proof for part (b)?

Answer 1

The matrix $M$ is skew symmetric if $M^T=-M$. A general skew symmetric 3x3 matrix has only 3 independent entries.

$$M=\left( \begin{array}{ccc} 0 & m_{12} & m_{13} \\ -m_{12} & 0 & m_{23} \\ -m_{13} & -m_{23} & 0 \\ \end{array} \right) $$

You can use the Rule of Sarrus to make sure $\det(M)=0$.

In a more general setting, the determinant of the skew symmetric $nxn$ matrix is $$\det(M)=\det(M^T)=\det(-M)=(-1)^n\det(M)$$ where we have used some basic properties of determinants. For odd $n$ this means $\det(M)=-\det(M)$ so $\det(M)=0$. This is sometimes called Jacobi's theorem after Carl Gustav Jacobi.

When $\det(M)=0$ the matrix is singular and the dimension of the column space must be less than $n$.

Further, if the 3x3 matrix $M$ above is $\neq \mathbf{0}$ at least one of $(m_{12},m_{13}, m_{23})$ must be nonzero. But as the entries come in pairs over the diagonal, setting one of them to a nonzero value means at least two columns are linearly independent (convince yourself by setting for example $m_{12}=1$ and notice that column 1 and column 2 are now linearly independent). Armed with this knowledge of 3x3 skew symmetric matrices we are ready to continue our adventure

Since $M$ is an odd dimension skew symmetric matrix the determinant is zero and the dimension of its column space $W$ is at most 2 (Jacobi's theorem). But since $M\neq 0$ and skew symmetric the dimension of $W$ must be at least 2. Hence the dimension of $W$ is exactly 2. This also means that at least two of the columns are $\neq \mathbf{0}$. We say that the columns of $M$, lets call them $(M_1,M_2,M_3)$, spans $W$.

The subgroup of orthogonal matrices with determinant +1 is called the special orthogonal group, denoted SO(3). Every rotation can be represented uniquely by an orthogonal matrix with unit determinant. We are free to pick ANY $A\in \text{SO(3)}$. Let $A$ be a proper $\frac{\pi}{2}$ rotation ($\det\,A=1)$ around a vector in the plane perpendicular to one of the nonzero columns $M_i=v$. The rotated vector $Av$ is clearly not in $W$.

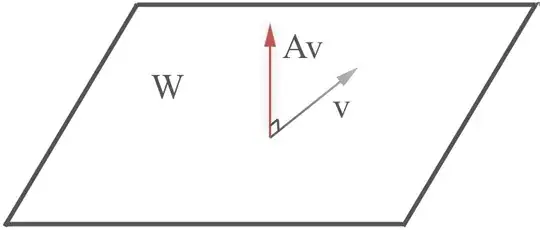
Hence, with our chosen rotation matrix $A$, at least one of the columns of the product $AM=[AM_1\,AM_2\,AM_3]$ has left $W$ completely. It is impossible for $AM$ to equal $cM$ where $c$ is a constant for this specific choice of $A$.