Average value of $\frac{x'A^2x}{x'A^3x}$ over surface of $n$-dimensional sphere

Question

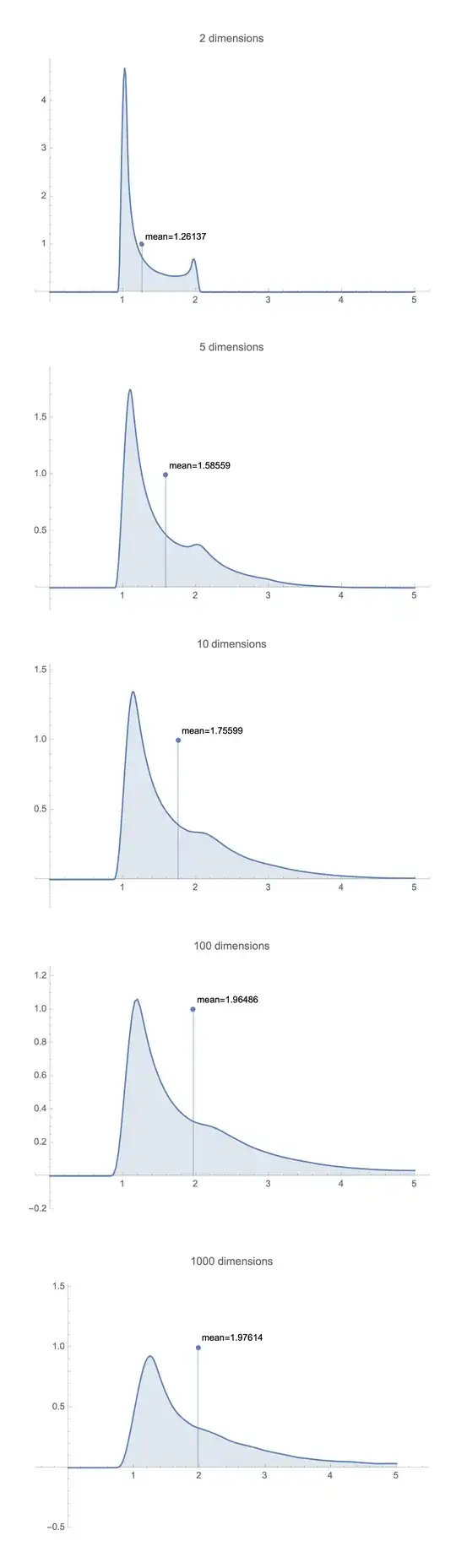
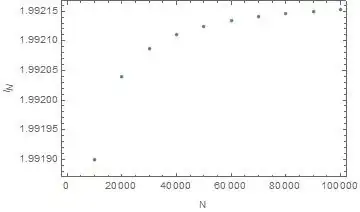
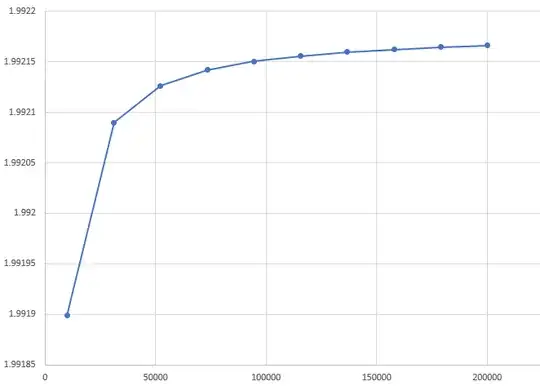
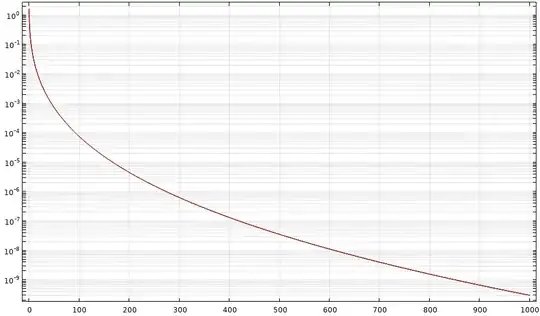
Suppose $A$ is a diagonal matrix with eigenvalues $1,\frac{1}{2},\frac{1}{3},\ldots,\frac{1}{n}$ and $x$ is drawn from standard Gaussian in $n$ dimensions. In numerical simulations, the following quantity seems to converge to $2$ as $n\rightarrow \infty$

$$z_n=E_{x\sim \mathcal{N}\left(0, I_n\right)}\left[\frac{x^T A^2 x}{x^T A^3 x}\right]$$

Can this be proven or disproven?

$z_n$ can also be written as the following sum

$$z_n=\sum_{i=1}^n i E_{y\sim \mathcal{N}\left(0,A^3\right)}\left[\frac{y_i^2}{\|y\|^2}\right]$$

This quantity can be viewed as the average ratio of quadratic forms $A^2$ and $A^3$ on the surface of $n$-dimensional sphere.

Here's what the distribution looks like for a few values of $n$, means are tending towards $2$

Answer 1

We can attempt to simplify this multidimensional integral as follows. The expression for the expectation value reads

$$E[\frac{x^TA^2 x}{x^TA^3 x}]=\int d^nx \frac{e^{-|x|^2/2}}{(2\pi)^{n/2}}\frac{\sum_{k=1}^n x^2_k/k^2}{\sum_{k=1}^n x^2_k/k^3}=:I_n$$

We insert the identity $\frac{1}{\Delta}=\int_0^{\infty}e^{-s\Delta}ds$, with $\Delta=\sum_{k=1}^n x^2_k/k^3$, to make the denominator disappear. The integrals over the random vector coordinates become Gaussian and we obtain the much simpler one-dimensional integral

$$I_n=\int_0^{\infty}ds F_n(s)G_n(s)~,~ F_n(s)=\prod_{k=1}^{n}\frac{1}{\sqrt{1+2s/k^3}}~,~ G_n(s)=\sum_{k=1}^n\frac{k}{k^3+2s}$$

The explicit forms for $F_{\infty}(s), G_{\infty}(s)$ are not very illuminating, but performing some quick integral asymptotics reveals that when $s\to\infty$

$$F_{\infty}(s)\sim \exp\left(-\frac{\pi}{\sqrt{3}}(2s)^{1/3}\right)$$ $$G_{\infty}(s)\sim \frac{2\pi}{3\sqrt{3}(2s)^{1/3}}$$

and since the sequences $F_n, G_n$ are monotonic and upper bounded by their respective infinite sum and product limits and those limits exist and the integral converges, we are allowed to use dominated convergence to take the limit inside the integral. Numerical integration for these functions for various values of $n$ indicates that the limit is most likely only approximating the value $2$ in the following manner:

Answer 2

I think this is covered, but not very accessible, in this paper from 1953 by Gurland on "Distribution of Quadratic Forms and Ratios of Quadratic Forms". It considers ratios for positive symmetric $Q$ and $P$ for: $$\frac{x^TQx}{x^TPx}$$

https://projecteuclid.org/journals/annals-of-mathematical-statistics/volume-24/issue-3/Distribution-of-Quadratic-Forms-and-Ratios-of-Quadratic-Forms/10.1214/aoms/1177728981.full

Also this reference may be of interest: https://www.researchgate.net/publication/224817325_Quadratic_Forms_in_Random_Variables_Theory_and_Applications

Edit:

(I didn't know of that other posting. My references above were redundant.)

I think @DinosaurEgg is right. I verified that integral by the one given in this reference (for integer exponents): https://www-2.rotman.utoronto.ca/~kan/papers/mupq.pdf

I also numerically integrated up to n=200000 and got the value 1.99217 It seems to stabilize to a value below 2.0 so most likely the value is not 2.0. I also provided some graphs below to build some level of confidence but certainly no proof.

Convergence (expectation vs. n):

Integrand (s<=1000, n=200000):

Log of Integrand (s<=1000, n=200000):

Answer 3

Not an answer, but wanted to point out an interesting result leading to an identity with the zeta functions. Let $A = \sum_{k\ge 1} X_k^2/k^2$ and $B = \sum_{k \ge 1}X_k^2/k^3$. Then a Taylor series expansion of $f(A, B)$ around $(\mu_A, \mu_B)=\mathbb{E}[(A, B)] = (\zeta(2), \zeta(3))$ is \begin{align*} \frac{A}{B} = \frac{\mu_A}{\mu_B} + \begin{pmatrix} 1/\mu_B \\ -\mu_A/\mu_B^2\end{pmatrix}^\intercal \begin{pmatrix} A - \mu_A \\ B - \mu_B \end{pmatrix} + \frac{1}{2}\begin{pmatrix} A - \mu_A \\ B - \mu_B \end{pmatrix}^\intercal\begin{pmatrix} 0 & -1/\mu_B^2 \\ -1/\mu_B^2 & 2 \mu_A/\mu_B^3 \end{pmatrix}\begin{pmatrix} A - \mu_A \\ B - \mu_B \end{pmatrix} + \cdots \end{align*} The first few terms of this expansion are \begin{align*} \mathbb{E}\left[\frac{A}{B}\right] &= \frac{\mu_A}{\mu_B} - \frac{\mathbb{E}(A - \mu_A)(B-\mu_B)}{\mu_B^2} + \frac{\mu_A\mathbb{E}(B-\mu_B)^2}{\mu_B^3} + \frac{\mathbb{E}(A-\mu_A)^2(B-\mu_B)}{6\mu_B^3} + \frac{\mathbb{E}(A-\mu_A)(B-\mu_B)^2}{3\mu_B^2} - \frac{\mathbb{E}(B-\mu_B)^3\mu_A}{2\mu_B^4} + \cdots \\ &= \frac{\zeta(2)}{\zeta(3)} - 2 \frac{\zeta(5)}{\zeta(3)^2} + 2 \frac{\zeta(6)\zeta(2)}{\zeta(3)^3} + \cdots \end{align*}