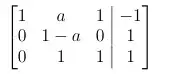0

I have this Matrix below: enter image description here

And they are asking for which values where a is missing solutions: And they are also asking for which values when a has inifinite many solutions. I have solved both cases with help of Gaussian:

enter image description here

and you can clearly see that when $1 - a = 1$ and that we have $a = 1$ it becomes $0 = a$ so when $a$ is $1$ the system is missing solutions.

but i also took the $\det(A)$ of the matrix and then i got this below: 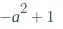enter image description here But the thing is that when the determinant is equal to 0 the matrix should have inifinite solutions and that is when $a$ is equal to $-1$ but it is also becomming $0$ when a is equal to $1$.

The thing is that when $a = 1$ it should not have any solutions but the determinant is also becomming zero after calculating the determinant i am very confused?? Can a such Matrix exist when we have a value that also says we have no solutions and on the same time also says that we have inifite many solutions when we calculate the determinant??

Jochen
  • 2,290
john
  • 195
  • Note that with $a=1$ you have according to the second row of your row reduced system that $0x+0y+0z=1$ which is of course false since zero is not equal to one. The punchline is that a determinant of zero implies that it is not the case that there is a single solution. It does not imply whether there are infinitely many or zero solutions however... making that distinction requires more careful analysis and both are possible. – JMoravitz Aug 05 '21 at 16:08
  • @JMoravitz Thanks :)! – john Aug 05 '21 at 16:49

0 Answers0