New updated code.
This seems to work better:
'''
angle between inner tangents between two intersecting ellipses, newer version
'''
import numpy as np
import math
import cmath
'''
####### FUNCTIONS IMPORTANT FOR THE CALCULATION #######
'''
def homogenize(x):
return np.array([x[0], x[1], 1])
transforming the vector of six coefficients
of a quadratic equation with two variables into a matrix of
the corresponding conic
def conic_from_equation(eq):
'''
eq is an np.array vector of the quadratic equation's six coefficients
eq[0]x2 + eq[1]xy + eq[2]y*2 + eq[3]x + eq[4]y + eq[5] = 0
conc is a symmetric matrix of the bilinier form of the quadratic equation
'''
return np.array([[2eq[0], eq[1], eq[3]],
[ eq[1], 2eq[2], eq[4]],
[ eq[3], eq[4], 2eq[5]]]) / 2
transformaing the matrix of a conic into a vector of six coefficients
of a quadratic equation with two variables
def equation_from_conic(C):
'''
c[0]x2 + c[1]xy + c[2]y*2 + c[3]x + c[4]y + c[5] = 0
'''
return np.array([C[0,0], 2C[0,1], C[1,1], 2C[0,2], 2C[1,2], C[2,2]])
obtaining the conic dual to a given conic,
both represented as symmetric 3x3 matrices
def dual_conic(conic):
return np.linalg.inv(conic)
given a pair of conics, as a pair of symmetric 3x3 matrices,
calculate the vector k = (k[0], k[1], k[2]) of values for each of which
the conic c1 - k[i]c2 from the pencil of conics c1 - tc2
is a degenerate conic (the anti-symmetric product of a pair of linear forms)
and also find the matrix U
of the projective transformation that simplifies the geometry of
the pair of conics, the geometry of the pencil c1 - t*c2 in general,
as well as the geometry of the three degenerate conics in particular
def trivialization_of(conic1, conic2):
'''
c1 and c2 are 3 by 3 symmetric matrices of two conics (possibly dual)
'''
c21 = np.linalg.inv(conic2).dot(conic1)
k, U = np.linalg.eig(c21)
return k, U
find the common points, i.e. points of intersection of a pair of conics
represented by a pair of symmetric matrices
def find_intersection_points(c1, c2):
k, U = trivialization_of(c1, c2)
L1 = (U.T).dot((c1 - k[0]c2).dot(U))
L2 = (U.T).dot((c1 - k[1]c2).dot(U))
x_0 = cmath.sqrt(-(L2[2,2] / L2[0,0]))
y_0 = cmath.sqrt(-(L1[2,2] / L1[1,1]))
sol = np.array([[ x_0, y_0, 1],
[-x_0, -y_0, 1],
[-x_0, y_0, 1],
[ x_0, -y_0, 1]])
sol = sol.dot(U.T)
return sol
find the three coefficients of all four common tangents to a pair of conics
make sure that the conics do have four common tangents,
which is the generic situation
def find_common_tangents(c1, c2):
dc1 = dual_conic(c1)
dc2 = dual_conic(c2)
return find_intersection_points(dc1, dc2)
if the two conics are ellipses, they do not intersect the line at infinity.
by polarity, the poles of the line at infinity are
the (affine and in fact metric) centers of the ellipses and are located
inside the ellipses each. We use them to detect the inner tangents and
to orient the vectors normal to these tangents in a way
so that the angle between these two normal vectors is the vector on the picture
def dual_to_infinity_line(conic):
p = dual_conic(conic).dot(np.array([0,0,1]))
return homogenize( p[0:2] / p[2] )
find the common inner tangents between a pair of conics,
represented as 3x3 symmetric matrices, with properly oriented normal vectors
def find_common_inner_tangents(c1, c2):
tn = find_common_tangents(c1, c2)
p1 = dual_to_infinity_line(c1)
p2 = dual_to_infinity_line(c2)
# boolean vector, true if inner tangent false if not
is_inner_tangent = np.logical_or(tn.real.dot(p1)tn.real.dot(p2) < 0, tn.imag.dot(p1)tn.imag.dot(p2) < 0)
tn = tn[ is_inner_tangent, : ]
# reorient one of the normal vectors so that they give us the proper angle
if tn.real[0,:].dot(p1)tn.real[1,:].dot(p1) > 0 or tn.imag[0,:].dot(p1)tn.imag[1,:].dot(p1) > 0:
tn[1,:] = - tn[1,:]
return tn
calculate the angle between a pair of line, given by their three coefficients
def angle_bn_C_lines(line1, line2):
theta = line1[0:2].dot(line2[0:2]) / ( cmath.sqrt( line1[0:2].dot(line1[0:2])*line2[0:2].dot(line2[0:2])) )
return cmath.acos(theta).conjugate()
calculate the proper angle between the inner or complex tangents of two quadratic equations
that represent a pair of conics, hopefully non-intersecting
def angle_bn_inner_tangents_of(eq_of_conic1, eq_of_conic2):
c1 = conic_from_equation(eq_of_conic1)
c2 = conic_from_equation(eq_of_conic2)
tn = find_common_inner_tangents(c1, c2)
return angle_bn_C_lines(tn[0,:], tn[1,:])
'''
####### END OF FUCTIONS IMPORTANT FOR THE CALCULATION #######
'''
'''
####### auxiliary functions to handle the test scenario:
'''
def cos_sin(angle_deg):
return math.cos(angle_degmath.pi/180), math.sin(angle_degmath.pi/180)
def rotation(cs_sn):
return np.array([[cs_sn[0], -cs_sn[1]],
[cs_sn[1], cs_sn[0]]])
def isom(angle, translation):
'''
isometry from global coordinate system (world system)
to conic-aligned coordinate system (conic attached)
'''
cos_, sin_ = cos_sin(-angle)
tr = - rotation((cos_, sin_)).dot(translation)
return np.array([[ cos_, -sin_, tr[0]],
[ sin_, cos_, tr[1]],
[ 0, 0, 1 ]])
calculating the conic defined by a pair of axes' lengths,
axes rotation angle and center of the conic
def Conic(major, minor, angle, center):
D = np.array([[minor**2, 0, 0],
[ 0, major**2, 0],
[ 0, 0, -(minormajor)*2]])
U = isom(angle, center)
return (U.T).dot(D.dot(U))
'''
####### end of auxiliary functions
'''
'''
test
'''
a1 = 5
b1 = 4.95
cntr1 = np.array([0,0])
w1 = 45
Eq1 = equation_from_conic(Conic(a1, b1, w1, cntr1))
Co1 = conic_from_equation(Eq1)
a2 = 1
b2 = .95
cntr2 = np.array([3,0])
w2 = 120
Eq2 = equation_from_conic(Conic(a2, b2, w2, cntr2))
Co2 = conic_from_equation(Eq2)
t4 = find_common_tangents(Co1, Co2)
print('all four tangents: ')
print(t4)
print('')
it = find_common_inner_tangents(Co1, Co2)
print('the inner tangents only: ')
print(it)
print('')
print('angle between inner tangents calculated by algorithm: ')
print( angle_bn_inner_tangents_of(Eq1, Eq2) )
print('')
print('angle calculation for circular approximation of the test case: ')
print('angle of internal tangents of a circle: ')
print(2cmath.asin((a1+a2)/cntr2[0]))
print('angle of external tangents of a circle: ')
print(2cmath.asin(abs(a1-a2)/cntr2[0]))
Previous code.
It seems like this code does what you want.
It treats the case of real inner tangents of disjoint ellipses or the case of two complex tangents of two ellipses, intersecting at two real points. For circles, the result seems to match the elementary formula.
'''
angle between inner tangents of two non-intersecting ellipses
or the complex angle between the two complex tangents of two
intersecting ellipses at two real points
'''
import numpy as np
import math
import cmath
'''
####### FUNCTIONS IMPORTANT FOR THE CALCULATION #######
'''
def homogenize(x):
return np.array([x[0], x[1], 1])
transforming the vector of six coefficients
of a quadratic equation with two variables into a matrix of
the corresponding conic
def conic_from_equation(eq):
'''
eq is an np.array vector of the equadratic equation's six coefficients
eq[0]x2 + eq[1]xy + eq[2]y*2 + eq[3]x + eq[4]y + eq[5] = 0
conc is a symmetric matrix of the bilinier form of the quadratic equation
'''
return np.array([[2eq[0], eq[1], eq[3]],
[ eq[1], 2eq[2], eq[4]],
[ eq[3], eq[4], 2eq[5]]]) / 2
transforming the matrix of a conic into a vector of six coefficients
of a quadratic equation with two variables
def equation_from_conic(C):
'''
c[0]x2 + c[1]xy + c[2]y*2 + c[3]x + c[4]y + c[5] = 0
'''
return np.array([C[0,0], 2C[0,1], C[1,1], 2C[0,2], 2C[1,2], C[2,2]])
obtaining the conic dual to a given conic,
both represented as symmetric 3x3 matrices
def dual_conic(conic):
return np.linalg.inv(conic)
given a pair of conics, as a pair of symmetric 3x3 matrices,
calculate the vector k = (k[0], k[1], k[2]) of values for each of which
the conic c1 - k[i]c2 from the pencil of conics c1 - tc2
is a degenerate conic (the symmetric tensor product of a pair of linear forms)
and also find the matrix U
of the projective transformation that simplifies the geometry of
the pair of conics, the geometry of the pencil c1 - t*c2 in general,
as well as the geometry of the three degenerate conics in particular
def trivialization_of(conic1, conic2):
'''
c1 and c2 are 3 by 3 symmetric matrices of two conics (possibly dual)
'''
c21 = np.linalg.inv(conic2).dot(conic1)
k, U = np.linalg.eig(c21)
return k, U
find the common points, i.e. points of intersection of a pair of conics
represented by a pair of symmetric matrices
def find_intersection_points(c1, c2):
k, U = trivialization_of(c1, c2)
L1 = (U.T).dot((c1 - k[0]c2).dot(U))
L2 = (U.T).dot((c1 - k[1]c2).dot(U))
acc = 1e-12
are_complex = (k.imag > acc).any()
if are_complex:
x_0 = cmath.sqrt(-L2[2,2] / L2[0,0])
y_0 = cmath.sqrt(-L1[2,2] / L1[1,1])
else:
x_0 = math.sqrt(abs(L2[2,2] / L2[0,0]))
y_0 = math.sqrt(abs(L1[2,2] / L1[1,1]))
sol = np.array([[ x_0, y_0, 1],
[-x_0, y_0, 1],
[-x_0, -y_0, 1],
[ x_0, -y_0, 1]])
sol = sol.dot(U.T)
return sol, are_complex
find the three coefficients of all four common tangents to a pair of conics
make sure that the conics do have four common tangents,
which is the generic situation
def find_common_tangents(c1, c2):
dc1 = dual_conic(c1)
dc2 = dual_conic(c2)
return find_intersection_points(dc1, dc2)
if the two conics are ellipses, they do not intersect the line at infinity.
by polarity, the poles of the line at infinity are
the (affine and in fact metric) centers of the ellipses and are located
inside the ellipses each. We use them to detect the inner tangents and
to orient the vectors normal to these tangents in a way
so that the angle between these two normal vectors is the vector on the picture
def dual_to_infinity_line(conic):
p = dual_conic(conic).dot(np.array([0,0,1]))
return homogenize( p[0:2] / p[2] )
find the common inner tangents between a pair of conics,
represented as 3x3 symmetric matrices, with properly oriented normal vectors
def find_common_inner_tangents(c1, c2):
tn, complex_tangents = find_common_tangents(c1, c2)
if not complex_tangents:
p1 = dual_to_infinity_line(c1)
p2 = dual_to_infinity_line(c2)
# boolean vector, true if inner tangent false if not
is_inner_tangent = ( tn.dot(p1)tn.dot(p2) < 0 )
tn = tn[ is_inner_tangent, : ]
# reorient one of the normal vectors so that they give us the proper angle
if tn[0,:].dot(p1)tn[1,:].dot(p1) > 0:
tn[1,:] = - tn[1,:]
else:
acc = 1e-12
is_complex_line = np.logical_or(abs(tn[:,0].imag) > acc,
abs(tn[:,1].imag) > acc,
abs(tn[:,2].imag) > acc)
tn = tn[ is_complex_line, :]
return tn, complex_tangents
calculate the angle between a pair of line, given by their three coefficients
def angle_bn_R_lines(line1, line2):
theta = line1[0:2].dot(line2[0:2]) / math.sqrt( line1[0:2].dot(line1[0:2])line2[0:2].dot(line2[0:2]))
return math.acos(theta) #180/np.pi
def angle_bn_C_lines(line1, line2):
theta = line1[0:2].dot(line2[0:2]) / ( cmath.sqrt( line1[0:2].dot(line1[0:2]))*cmath.sqrt(line2[0:2].dot(line2[0:2])) )
return cmath.acos(theta)
calculate the proper angle between the inner or complex tangents of two quadratic equations
that represent a pair of conics, hopefully non-intersecting
def angle_bn_inner_tangents_of(eq_of_conic1, eq_of_conic2):
c1 = conic_from_equation(eq_of_conic1)
c2 = conic_from_equation(eq_of_conic2)
tn, complex_tangents = find_common_inner_tangents(c1, c2)
if complex_tangents:
return angle_bn_C_lines(tn[0,:], tn[1,:])
else:
return angle_bn_R_lines(tn[0,:], tn[1,:])
'''
####### END OF FUCTIONS IMPORTANT FOR THE CALCULATION #######
'''
'''
####### auxiliary functions to handle the test scenario:
'''
def cos_sin(angle_deg):
return math.cos(angle_degmath.pi/180), math.sin(angle_degmath.pi/180)
def rotation(cs_sn):
return np.array([[cs_sn[0], -cs_sn[1]],
[cs_sn[1], cs_sn[0]]])
def isom(angle, translation):
'''
isometry from global coordinate system (world system)
to conic-aligned coordinate system (conic attached)
'''
cos_, sin_ = cos_sin(-angle)
tr = - rotation((cos_, sin_)).dot(translation)
return np.array([[ cos_, -sin_, tr[0]],
[ sin_, cos_, tr[1]],
[ 0, 0, 1 ]])
calculating the conic defined by a pair of axes' lengths,
axes rotation angle and center of the conic
def Conic(major, minor, angle, center):
D = np.array([[minor**2, 0, 0],
[ 0, major**2, 0],
[ 0, 0, -(minormajor)*2]])
U = isom(angle, center)
return (U.T).dot(D.dot(U))
'''
####### end of auxiliary functions
'''
#%%
'''
Example of finding the angle between the common tangents of a pair of conics:
conic 1 (circle): major axis = 2, minor axis = 2, angle = 0, center = (0,0)
conic 2 (circle): major axis = 3, minor axis = 3, angle = 0, center = (4,0)
'''
a = 2
b = 2
cntr = np.array([0,0])
w = 0
Eq1 = equation_from_conic(Conic(a, b, w, cntr))
Co1 = conic_from_equation(Eq1)
a = 3
b = 3
cntr = np.array([4,0])
w = 0
Eq2 = equation_from_conic(Conic(a, b, w, cntr))
Co2 = conic_from_equation(Eq2)
four_tngs = find_common_tangents(Co1, Co2)
#inner_tngs = find_common_inner_tangents(Co1, Co2)
print( angle_bn_inner_tangents_of(Eq1, Eq2) )
print(2*cmath.asin((2+3)/4))
$$$$
Older Post.
Today I had some time to experiment with the code I wrote in the previous post. Theoretically, the approach should be exactly the same as the case of four real tangents. However, the only major hassle I am seeing for now is the complex arithmetic. In the function find_common_points() some square roots are calculated, which works fine for real numbers, but when the entries of the trivialized degenerate conics L1 and L2 become complex (and they do in the case of two ellipses intersecting at exactly two points), then one needs to carefully calculate the appropriate complex square root. The rest is the same. With two complex tangents and two real ones, you choose the complex to be "inner" and calculate a complex dot product divided by complex norms, which will give you a complex number. After that you can take complex arccos() of that. Whether this scheme leads to the same elementary circle calculation you show in your post, is unclear for now, although the fact that all of these are complex holomorphic functions of several variables that overlap in the real case suggest that it is possible these constructions match due to the rigidity of holomorphic prolongations.
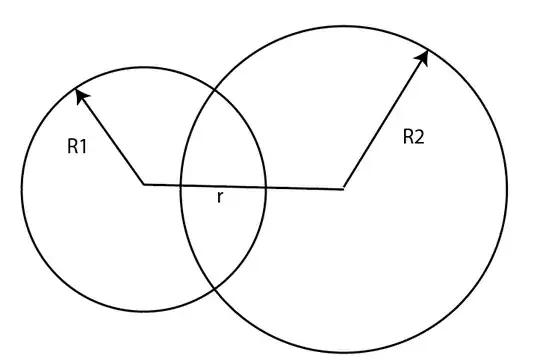
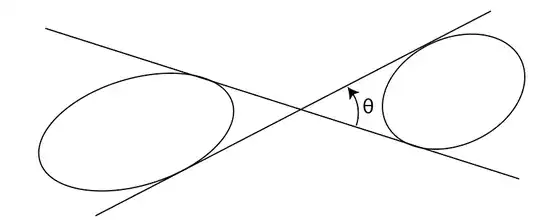
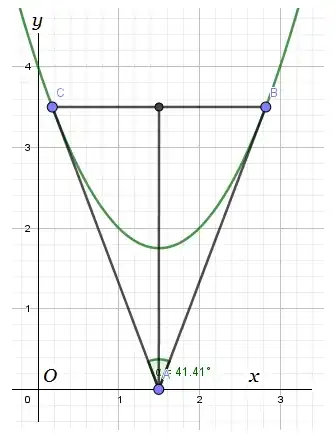
However, if one is interested in checking if their solution is correct then they can take the major and minor axes length of ellipse equal so that the ellipse decomposes into a circle. And we have a formula for the determination of that angle for a circle.
Iterative method (Section C): https://arc.aiaa.org/doi/pdf/10.2514/1.G002932
– Kashish Dhal Jul 31 '21 at 22:21