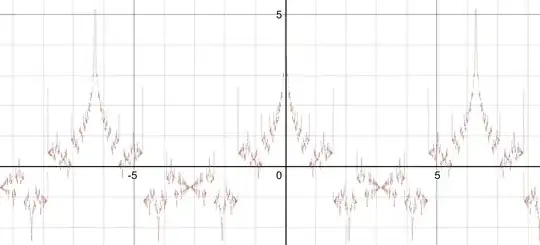
Here is what the fractal looks like on desmos; you can change the width of the function for more detail desmos fractal This is the
for the question. I will use this inverse tangent generalization, polar coordinates and the signum function. Note that I cannot solve for y in closed form and that $\mathrm{k\Bbb Z=kZ,Z\in\Bbb Z}$. We would like to find out a fractal dimension for $0\le\theta\le2\pi$: $$\mathrm{r=\sum_{n=1}^\infty \frac{sgn(sec(n\theta))}{n}\implies \sqrt{x^2+y^2}=\sum_{n=1}^\infty\frac{sgn\left(sec\left(n\,tan^{-1}\left(\frac yx\right)+kn\Bbb Z\right)\right)}{n}\implies y=\pm\sqrt{\left(\sum_{n=1}^\infty\frac{sgn\left(sec\left(n\,tan^{-1}\left(\frac yx\right)+kn\Bbb Z\right)\right)}{n}\right)^2-x^2}= \pm\sqrt{\left(\sum_{n=1}^\infty\frac{sgn\left(sec\left(n\,tan^{-1}\left(\frac {\pm\sqrt{\left(\sum_{n=1}^\infty\frac{sgn\left(sec\left(n\,tan^{-1}\left(\frac {…}{x}\right)+kn\Bbb Z\right)\right)}{n}\right)^2-x^2}}{x}\right)+kn\Bbb Z\right)\right)}{n}\right)^2-x^2}}$$
Notice the “stable” points of interest at around (x,y) at ($\infty$,0),(0,0),(.7,0),(0,$\pm$ .41), and (0,$\pm$1.1). There also appear to be 2 asymptotes of $\theta=\pm\frac\pi3\implies y=\pm\sqrt3x$ Here is what the fractal looks like up to n=1000 for the truncated sum. Firstly is a cartesian plot:
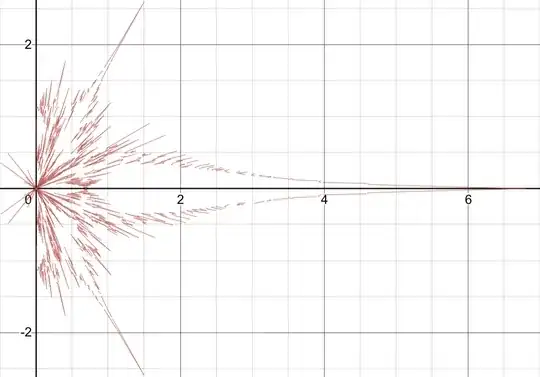
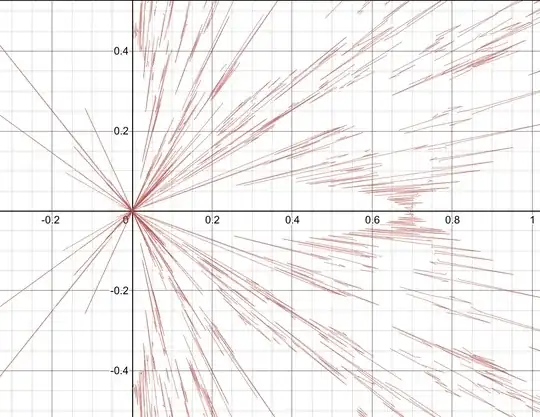
Zoomed in polar plot of “chaotic” section:
The full polar area of the fractal from $0\le\theta\le 2\pi$ diverges, but the primitive area formula can be written in terms of digamma functions: $$\mathrm{A=\frac12\int\sum_{n=1}^\infty\sum_{m=1}^\infty\frac{sgn(sec(m\theta)sgn(sec(n\theta))}{mn}d\theta=\frac{\theta}2\left(\sum_{n=1}^\infty\frac{sgn(sec(n \theta))}n\right)^2}$$
Although there are many types of fractal dimensions, this one probably does not have an easy solution for the dimension. I would like a fractal dimension in exact form as there is little hope for a closed form solution. Besides this, any interesting information about the fractal itself is appreciated. There is also the possibility of r=r($\theta$) not being a fractal. Please correct me and give me feedback!