Fractal dimension of the function $f(x)=\sum_{n=1}^{\infty}\frac{\mathrm{sign}\left(\sin(nx)\right)}{n}$

Question

Consider the function $$ f(x)=\sum_{n=1}^{\infty}\frac{\mathrm{sign}\left(\sin(nx)\right)}{n}\, . $$ This is a bizarre and fascinating function. A few properties of this function that SEEM to be true:

1) $f(x)$ is $2\pi$-periodic and odd around $\pi$.

2) $\lim_{x\rightarrow \pi_-} f(x) = \ln 2$. (Can be proven by letting $x = \pi-\epsilon$, expanding the sine function, and taking the limit as $\epsilon\rightarrow 0$.)

3) $\int_0^{\pi}dx\, f(x) = \frac{\pi^3}{8}$ (Can be "proven" by integrating each $\mathrm{sign}\left(\sin(nx)\right)$ term separately. Side question: Is such a procedure on this jumpy function even meaningful?)

All of this despite the fact that I can't really prove that this function converges anywhere other than when $x$ is a multiple of $\pi$!

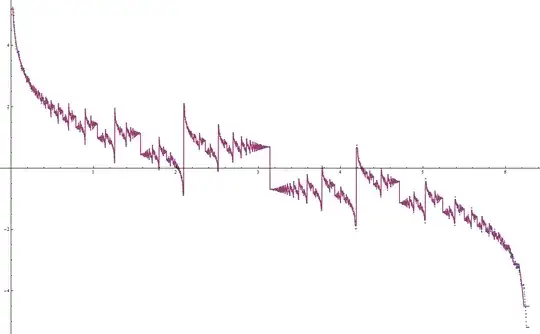
A graph of this function (e.g. in Mathematica) reveals an amazing fractal shape. My question: What is the fractal dimension of the graph of this function? Does the answer depend on which definition of fractal dimension we use (box dimension, similarity dimension, ...)?

This question doesn't come from anywhere other than from my desire to see if an answer exists.

As requested, a plot of this function on the range $x\in[0,2\pi]$:

Edited to add:

Other, perhaps more immediate, questions about this function:

1) Does it converge? Conjecture: It converges whenever $x/\pi$ is irrational, but doesn't necessarily diverge if $x/\pi$ is rational. See, e.g., $x = \pi$, where it converges to zero, and apparently to $\pm \ln 2$ on either side of $x = \pi$.

2) I would guess that it diverges as $x\rightarrow 0_+$. How does it diverge there? If this really is a fractal function, I would suppose that the set of points where it diverges is dense. For instance, it appears to have a divergence at $x = 2\pi/3$.

Edit 2:

Another thing that's pretty straightforward to prove is that: $$ \lim_{x\rightarrow {\frac{\pi}{2}}_-} f(x) = \frac{\pi}{4} + \frac{\ln 2}{2} $$ and $$ \lim_{x\rightarrow {\frac{\pi}{2}}_+} f(x) = \frac{\pi}{4} - \frac{\ln 2}{2} $$

Final Edit:

I realize now that the initial question about this function - what is its fractal dimension - is (to use a technical term) very silly. There are much more immediate and relevant question, e.g. about convergence, etc. I've already selected one of the answers below as answering a number of these questions.

One final point, for anyone who stumbles on this post in the future. The term $\mathrm{sign}(\sin(nx))$ is actually a square wave, and so we can use the usual Fourier series of a square wave to derive an alternate way of expressing this function: $$ f(x)=\sum_{n=1}^{\infty}\frac{\mathrm{sign}\left(\sin(nx)\right)}{n} = \frac{4}{\pi}\sum_{n=1}^{\infty}\sum_{m=1}^{\infty} \frac{\sin(n(2m-1)x)}{n(2m-1)} $$ By switching the order of the sums and doing the $n$ sum first, this could also be represented as a weighted sum of sawtooth waves.

Answer 1

We can prove the convergence almost everywhere using the following

Theorem: Let $\varphi $ a function such that $$\varphi\left(x\right)\in L^{2}\left(-\pi,\pi\right),\,\varphi\left(x+2\pi\right)=\varphi\left(x\right),\,\int_{0}^{2\pi}\varphi\left(x\right)dx=0.$$ Assume that $$\sup_{0<h\leq\delta}\left(\int_{0}^{2\pi}\left|\varphi\left(x+h\right)-\varphi\left(x\right)\right|^{2}dx\right)^{1/2}=O\left(\delta^{1/2}\right) $$ and let the sequence of real numbers $\left(a_{n}\right)_{n} $ such that $$\sum_{n\geq2}a_{n}^{2}\log^{\gamma}\left(n\right)<\infty,\,\gamma>3 $$ then the series $$\sum_{n\geq1}a_{n}\varphi\left(nx\right) $$ converges almost everywhere.

(For a reference see V. F. Gaposhkin, “On series relative to the system $\left\{ \varphi\left(nx\right)\right\} $”, Mat. Sb. (N.S.), $69(111)$:$3$ ($1966$), $328–353$)

So it is sufficient to note that $\varphi\left(x\right)=\textrm{sign}\left(\sin\left(x\right)\right) $ verifies the conditions and $$\sum_{n\geq2}\frac{\log^{\gamma}\left(n\right)}{n^{2}}<\infty $$ for all $\gamma>0 $. So we have that $$\sum_{n\geq1}\frac{\textrm{sign}\left(\sin\left(nx\right)\right)}{n}. $$ converges almost everywhere.

At zero an heuristic argument can be that for all $M>0 $ exists some $\delta>0 $ such that, if $0<x<\delta $, we have $$M<\sum_{n\geq1}\frac{\textrm{sign}\left(\sin\left(nx\right)\right)}{n}$$ because if $x$ is “small” we have $\textrm{sign}\left(\sin\left(nx\right)\right)=1$ and so, since $\sum_{n\geq1}\frac{1}{n}$ diverges, we can find a sufficient small $\delta$ such that the series is bigger than every fixed $M$ and the negative contributions are too “small” for a significant cancellation.

Answer 2

The series certainly converges when $x$ is a rational multiple of $\pi$, say $x=p\pi/q$ where $p/q$ is in lowest terms. Here is an outline of a proof of this using Dirichlet's test.

The numbers $$\alpha_k = k\,\pi\frac{p}{q} \mod 2\pi$$ form a group under addition. In particular, each element $\alpha$ has an additive inverse $\beta$ with the property that $\sin(\alpha)=-\sin(\beta)$. As a result, the sequence $(\alpha_k)_k$ is periodic with the same number of positive and negative ones in a period. Thus, if we define $$b_n = \text{sign}(\sin(n\pi p/q)),$$ it's easy to see that the sequence $$S_N = \sum_{n=1}^N b_n$$ is bounded. We can now apply Dirichlet's test (as stated in the link above) using $a_n=1/n$.

I suspect that a similar argument will work for irrational multiples of $\pi$ using uniform distribution of $nx\mod 2\pi$. I also suspect that such an argument might be very hard and depend on how well approximable $x/\pi$ is by rationals.

Returning to rational multiples of $\pi$, these types of sequences can be computed in closed form using various tricks involving transforms of the harmonic sequence. At $x=\pi/2$, for example, the series reduces to $$\sum_{n=0}^{\infty} \frac{(-1)^{n}}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots = \frac{\pi}{4}.$$ At $x=2\pi/3$, the sum is $$\sum _{n=0}^{\infty } \left(\frac{1}{3 n+1}-\frac{1}{3 n+2}\right) = \frac{\pi }{3 \sqrt{3}}.$$ There is a key difference between these two series, however. For the first we have $$\left\{\text{sign}(\sin(n\pi/2))\right\}_{n=1,2,3,4} = \{1,0,-1,0\}.$$ which has two zeros. Numbers close to $\pi/2$ but just a little less will start with the pattern $\{1,1,-1,-1\}$. Numbers very close to and less than $\pi/2$ will maintain this pattern in the sum for a long time and result in a sum that's close to $$\sum _{n=0}^{\infty } \left(\frac{1}{4 n+1}+\frac{1}{4 n+2}-\frac{1}{4 n+3}-\frac{1}{4 n+4}\right) = \frac{1}{4} (\pi +\log (4)) \approx 1.13197.$$ Numbers close to $\pi/2$ and just above will yield a sum close to $$\sum _{n=0}^{\infty } \left(\frac{1}{4 n+1}-\frac{1}{4 n+2}-\frac{1}{4 n+3}+\frac{1}{4 n+4}\right) = \frac{1}{4} (\pi -\log (4)) \approx 0.438825.$$ This leads to the appearance of a jump discontinuity at $\pi/2$ where the actual value is, in fact, between the two.

For $x=2\pi/3$, by contrast, we have $$\left\{\text{sign}(\sin(2n\pi/3))\right\}_{n=1,2,3} = \{1,-1,0\},$$ which has just one zero. For values of $x$ close to $2\pi/3$ but just a little less, the sequence starts $\{1,-1,-1\}$ and we can make the partial sums as large in absolute value as we like (but negative) by choosing $x$ to be sufficiently close to $2\pi/3$. On the other side of $2\pi/3$ the sequence is $\{1,-1,1\}$ and we have similar but positive behavior. This leads to the appearance of an asymptote like feature at $2\pi/3$.

Note that these arguments are not complete. The argument near $2\pi/3$ is very much like Marco's argument near zero. Detailed analysis for irrational multiples of $\pi$ is likely to be quite sensitive and require a strong knowledge of uniform distribution of sequences mod $2\pi$. I also suspect that both behaviors are genuine and dense in the real line.

Finally, I don't think that fractal dimension is a reasonable concept to apply here. While certain parts of the graph look like other parts, self-similar sets and their generalizations are compact sets. This set is neither closed nor bounded. Neither similarity dimension nor box-counting dimension will be well-defined here. Hausdorff dimension will, I suppose, be defined. I don't think it's likely to be easy to compute, though. The Hausdorff dimension of Weiestrass's function is an open question.

Answer 3

Although I've already selected one of the excellent answers above, I thought I'd post an answer that I figured out to one of the questions I posed in the original post, namely: "I would guess that it diverges as $x\rightarrow 0_+$. How does it diverge there?"

So, as noted above, the term $\mathrm{sign}(\sin(n x))$ is a square wave with period $2\pi/n$. Suppose $x/\pi$ is irrational. Then $\mathrm{sign}(\sin(n x))$ is always -1 or +1, never 0. Define $$ \phi(x,k) = \left\lfloor \frac{k\pi}{x} \right\rfloor $$ as the largest integer such that $\phi(x,k) \, x < k \pi$. Defining $H_m$ as the $m^{\mathrm{th}}$ harmonic number, the original series can then be divided into finite positive and negative subsequences of terms of the form $\pm 1/n$ and rewritten as \begin{align} f(x) &= \sum_{n = 1}^{\phi(x,1)} \frac{1}{n} \;-\;\sum_{n = \phi(x,1)+1}^{\phi(x,2)} \frac{1}{n} \;+\;\sum_{n = \phi(x,2)+1}^{\phi(x,3)} \frac{1}{n} \;-\; ...\\ &= H_{\phi(x,1)} - \left(H_{\phi(x,2)} - H_{\phi(x,1)}\right)+ \left(H_{\phi(x,3)} - H_{\phi(x,2)}\right) - ...\\ &= H_{\phi(x,1)} \;+\; \sum_{n = 1}^{\infty}{(-1)}^n\left(H_{\phi(x,n+1)} - H_{\phi(x,n)}\right) \end{align} for irrational $x/\pi$. In fact, this last expression can be used to calculate the original function. Although this harmonic number representation is ostensibly only valid for irrational $x/\pi$, it seems to overlay the original function very nicely, as shown below:

Now, as to the divergence for small $x$. When $x$ is small, $\phi(x,n)$ becomes large, and we have \begin{align} H_{\phi(x,n)}&\approx \ln\left(\phi(x,n)\right) + \gamma\\ &= \ln\left(\left\lfloor \frac{n\pi}{x} \right\rfloor\right) + \gamma\\ &\approx \ln\left(\frac{n\pi}{x}\right) + \gamma\, . \end{align} The above expression for $f(x)$ then reduces to $$ f(x) \approx \ln\left(\frac{\pi}{x}\right) + \gamma + \sum_{n=1}^{\infty}{(-1)}^n \ln\left(1 + \frac{1}{n}\right)\, , $$ where \begin{align} \sum_{n=1}^{\infty}{(-1)}^n \ln\left(1 + \frac{1}{n}\right) &= \ln\left(\prod_{n=1}^{\infty}\left(1 - \frac{1}{4n^2}\right)\right)\\ &= \ln\left(\frac{2}{\pi}\right)\qquad \text{By the Wallis product}\, . \end{align} The small-$x$ approximation then reduces to $$ f(x) \approx -\ln x \;+\; \gamma \;+\; \ln 2\, . $$ This is plotted below along with the original function. So the answer is: A logarithmic divergence as $x\rightarrow 0_+$.