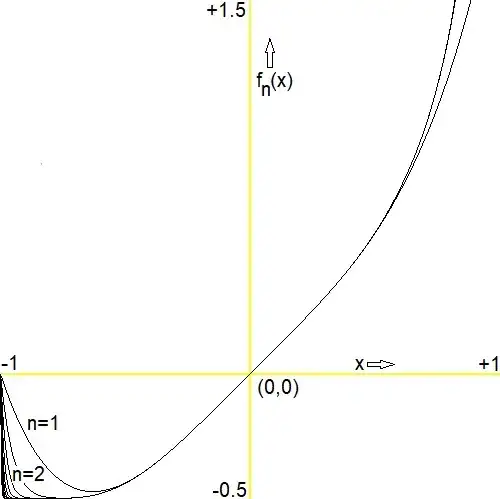
This post is sort of followup of
Prove or disprove that the function is convex,
a question coined up by Erik Satie.
Define $f_n(x)=\sum_{k=1}^{2n}x^{k^2}$ where $n\ge 1$ a natural number and $-1 \leq x \leq 1$.
From the picture below the fact seems evident but I have no idea how to prove it (otherwise).
So, prove or disprove that $f_n(x) \gt -1/2$.
Some easy to prove facts about the function behaviour are noticed: $$ \begin{cases} f_n(-1) = 0 & ; & f_n'(-1) = \sum_{k=1}^{2n} (-1)^{k-1} k^2 = -2n^2-n \lt 0 \\ f_n(0)=0 & ; & f_n'(0) = 1 \\ f_n(+1)=2n & ; & f_n'(+1) = \sum_{k=1}^{2n} k^2 = 2n(2n+1)(4n+1)/6 \end{cases} $$ Numerically:
n = 1 ; minimum = -4.72466351692463E-0001 at x = -6.31262525050100E-0001 n = 2 ; minimum = -4.98653787376657E-0001 at x = -7.51503006012024E-0001 n = 3 ; minimum = -4.99936871867468E-0001 at x = -8.11623246492986E-0001 n = 4 ; minimum = -4.99997098383334E-0001 at x = -8.47695390781563E-0001 n = 5 ; minimum = -4.99999866659599E-0001 at x = -8.71743486973948E-0001 n = 6 ; minimum = -4.99999993940378E-0001 at x = -8.91783567134269E-0001 n = 7 ; minimum = -4.99999999732976E-0001 at x = -9.03807615230461E-0001 n = 8 ; minimum = -4.99999999987309E-0001 at x = -9.15831663326653E-0001 n = 9 ; minimum = -4.99999999999449E-0001 at x = -9.23847695390782E-0001 n = 10 ; minimum = -4.99999999999967E-0001 at x = -9.31863727454910E-0001 n = 11 ; minimum = -4.99999999999999E-0001 at x = -9.35871743486974E-0001 n = 12 ; minimum = -5.00000000000000E-0001 at x = -9.39879759519038E-0001