Prove or disprove that the function is convex .

Question

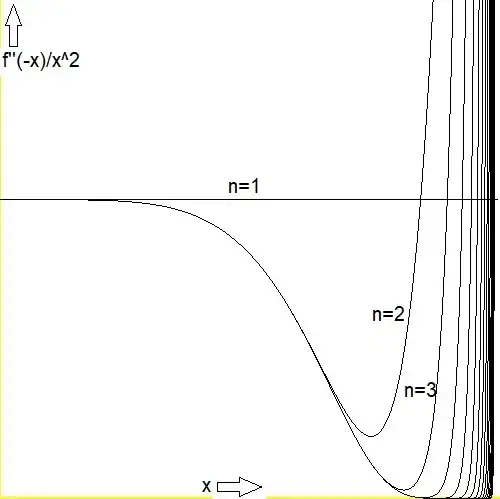
It seems we have :

Define $\displaystyle f(x)=\sum_{k=1}^{2n}x^{k^2}$ where $n\geq 1$ a natural number and $-1\leq x\leq 1$

Claim :

$f''(x)\geq 0$

My attempt :

The case $n=1$ is trivial . So I have tried to show by induction but it doesn't works because the the sum of the two last terms have a negative second derivative on $(-1+\varepsilon_n,0)$ and $\varepsilon_n>0$.

Edit the case $n=2$ :

Using Jensen's definition and factoring we have :

$$ (x - y)^2 (32767 x^{14}+ 65518 x^{13} y + 98149 x^{12}y^2 + 130220 x^{11} y^3 + 160471 x^{10} y^4 + 186354 x^9 y^5 + 204229 x^8 y^6 + 210664 x^7 y^7 + 32640 x^7 + 204229 x^6 y^8 + 64128 x^6 y + 186354 x^5 y^9 + 91008 x^5 y^2 + 160471 x^4 y^{10} + 107136 x^4 y^3 + 130220 x^3 y^{11} + 107136 x^{3} y^4 + 98149 x^2 y^{12} + 91008 x^2 y^5 + 28672 x^2 + 65518 x y^{13} + 64128 x y^6 + 40960 x y + 32767 y^{14} + 32640 y^7 + 28672 y^2)\geq 0$$

For $-0.5\leq x\leq-0.4$ and $-0.5\leq y\leq-0.4$ because we have :

$$32767 x^{14}+ 65518 x^{13} y + 98149 x^{12}y^2 + 130220 x^{11} y^3 + 160471 x^{10} y^4 + 186354 x^9 y^5 + 204229 x^8 y^6 + 210664 x^7 y^7\geq 0$$

$$f(x,y)=-(32640 x^7+64128 x^6 y +91008 x^5 y^2+107136 x^4 y^3+91008 x^2 y^5+107136 x^{3} y^4 +32640 y^7+64128 x y^6)\leq f(-0.5,-0.5)<2\cdot28672\cdot0.4^2<\leq 28672(x^2+y^2)$$

Edit 2 :

It seems we can build a proof by induction playing with $x^4$ on $(-1+\varepsilon_n,0)$ and $\varepsilon_n>0$ we have something like :

$$\left(x^4C_n+\sum_{k=2}^{2n-2}x^{k^2}\right)’’\geq0$$

And :

$$\left(x^4(1-C_n)+x^{(2n-1)^2}+x^{(2n)^2}\right)''\geq 0$$

Remains to find $0<C_n<1$ a real number depending on $n$

Edit 3: It seems we can take $C_n=\frac{\left(n\right)!-1}{n!}$ always on $(-1+\varepsilon_n,0)$ and $\varepsilon_n>0$ .

How to show it ?

See https://math.stackexchange.com/questions/112833/convexity-of-thetaq — Barackouda, Jul 12 '21 at 15:10
Not sure if helpful, but from checking a few examples, it seems like $f''(x) \geq x^{(2n)^2}$ for $x \in [-1,1]$ holds in general. — jasnee, Jul 12 '21 at 15:27
The last two terms have a negative second derivative??? What is the second derivative of $x^{k^2}$??? — David C. Ullrich, Jul 12 '21 at 17:06
@DavidC.Ullrich No not on the hardest part wich is $I=(-1,0)$ — Barackouda, Jul 13 '21 at 13:39
@ClaudeLeibovici Can you confirm it for small value ? Thanks ! — Barackouda, Jul 14 '21 at 09:57
Equivalently we wish to prove that $\sum\limits_{k=2}^{2n}(k^4-k^2)(-x)^{k^2-4}\ge0$ for all $n>1$ and $0<x<1$. — TheSimpliFire, Jul 15 '21 at 10:05
Whatever you are doing, but where do you compute the second derivative in case $n=2$?? What are $x$ and $y$ ? — daw, Jul 15 '21 at 14:38
@daw It's the Jensen's definition of the convexity + continuity and I use Wolfram alpha . — Barackouda, Jul 15 '21 at 14:54
@TheSimpliFire: Shouldn't that be $\sum\limits_{k=2}^{2n}(k^4-k^2)(-x)^{k^2-\color{red}{2}}\ge 0$ for all $n\ge 1$ and $0\le x\le 1$ ? — Han de Bruijn, Jul 17 '21 at 20:14
@HandeBruijn your guys's expressions differ multiplicatively by $x^2$, so I don't see why it matters — mathworker21, Jul 18 '21 at 08:09
@mathworker21: Ah, yes, of course, that's the simplifired version :-) — Han de Bruijn, Jul 18 '21 at 11:44
@ErikSatie: I've posted a followup of this interesting question: Prove or disprove that $f_n(x)\gt -1/2$ — Han de Bruijn, Jul 18 '21 at 20:31
@TymaGaidash: No, formatting is correct. It looks good at our Windows 10 PC, but the same weird results as yours are obtained (with Safari) at our Apple iPad. — Han de Bruijn, Jul 20 '21 at 19:45

Han de Bruijn · Answer 1 · 2021-07-18T18:58:04.223

0

Employing the SimpliFired version of the problem gives the following pictorial comment.
Scale in $y$-direction is $10$ times the one in $x$-direction.

Ipse est: $\,\sum\limits_{k=2}^{2n}(k^4-k^2)(-x)^{k^2-4}\ge0\,$ for $\,n\ge 1\,$ and $\,0\le x \le 1\,$.
Or does it count as a proof without words?

edited Jul 18 '21 at 18:58

answered Jul 18 '21 at 12:06

Han de Bruijn

17,475

9

Well, rather count it as a Plausible sketch without proof ... – Hanno Jul 18 '21 at 12:21
@Hanno: Isn't that comment and its upvotes a bit predictable in some circles? The above picture without doubt would count as a proof in an environment with physicists. – Han de Bruijn Jul 20 '21 at 19:49
@HandeBruijn those physicists would be wrong – mathworker21 Jul 24 '21 at 02:47

Prove or disprove that the function is convex .

1 Answers1

Linked