11

Given vectors $x_1,...,x_n\in\Bbb R^d$. The conic span of these vectors is

$$\mathrm{cone}\{x_1,...,x_n\}:=\{\alpha_1 x_1+\cdots +\alpha_n x_n\mid \alpha_1,...,\alpha_n\ge 0\}.$$

Question: Is there a "simple" explicit formula for computing the volume of $\mathrm{cone}\{x_1,...,x_n\}\cap \Bbb B^n$, where $\Bbb B^n$ is the unit ball centered at the origin?

$\mathrm{Vol}$ indicates the volume that I am interested in.

M. Winter
  • 30,828
  • What do you mean by simple? Simple to write down is sufficient enough, or must it be simple to compute? – AB Balbuena Jun 22 '21 at 01:20
  • 1
    @ABBalbuena I need it for theoretical purpose, so I am not so much interested in computational efficiency. I am looking for a formula that is "easy to work with", but of course this is still vague. – M. Winter Jun 22 '21 at 01:21

1 Answers1

9

A theorem by Ribando (Measuring Solid Angles Beyond Dimension Three, Discrete Comput Geom 36:479–487 (2006)), which is a rediscovery of a result of Aomoto (Analytic structure of Schlafli function, Nagoya Math. J. 68:1-16 (1977)), is described by Beck, Robins and Sam (Positivity Theorems for Solid-Angle Polynomials, Beitrage zur Algebra und Geometrie, Vol. 51, No. 2, 493-507 (2010)) as a way to compute the solid angle at the vertex of a polyhedral cone. Ribando's result is stated as follows:

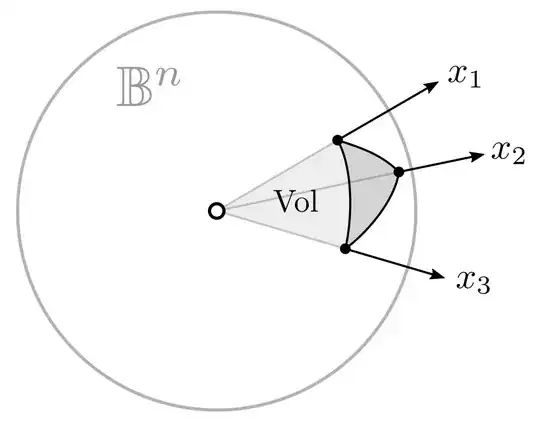
Let $\Omega \subseteq \Bbb{R}^n$ be a solid-angle spanned by unit vectors $\lbrace v_1 , \dots , v_n \rbrace$, let $V$ be the matrix whose ith column is $v_i$ , and let $\alpha _{ij} = v_i \cdot v_j$ as above. Let $T_{\alpha}$ be the following infinite multivariable Taylor series: $$T_{\alpha} = \dfrac{det \ V}{(4 \pi )^{n/2}} \sum _{a \in \Bbb{N}^{{n \choose 2}}} \left[ \dfrac{(-2)^{\sum _{i < j} a_{ij}}}{ \Pi _{i<j} a_{ij}!} \Pi _{i} \Gamma \left( \dfrac{1 + \sum _{m \neq i} a_{im}}{2} \right) \right] \alpha^{a}$$ The series $T_{\alpha}$ agrees with the normalized measure of solid-angle $\Omega$ whenever $T_{\alpha}$ converges.

Here the solid angle refers to the limit as $r \rightarrow 0$ of the volume of the intersection of the polyhedral cone with with the ball of radius $r$ divided by the volume of the ball of radius $r$ .

AB Balbuena
  • 410
  • That is spot on, thank you! Is there anything to be said about when this converges? – M. Winter Jun 22 '21 at 08:50
  • The factorial in the denominator, is it to be interpreted as a Gamma function? And am I interpreting it correctly that the factorial is applied to each factor, not to the whole product? – M. Winter Jun 22 '21 at 16:32
  • I've dug up Ribando's paper. From the proof of the formula, it does seem that the factorial is applied to each factor. Theorem 3.2 gives bounds for the domain of convergence. https://link.springer.com/content/pdf/10.1007/s00454-006-1253-4.pdf – AB Balbuena Jun 23 '21 at 00:20