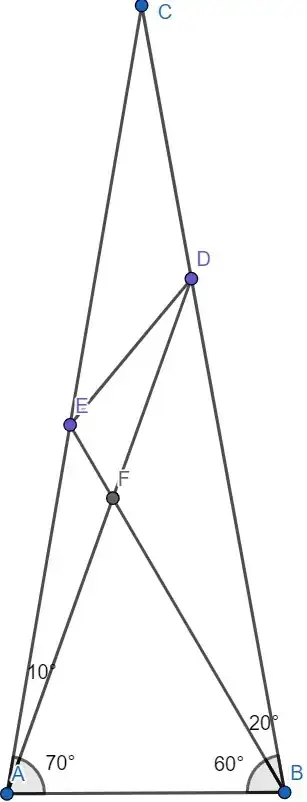
In $\Delta ABC$, $\angle EAF=10^{\circ}$, $\angle FAB=70^{\circ}$, $\angle FBA=60^{\circ}$, $\angle DBF=20^{\circ}$. The goal is to find $\angle EDA$.
I have tried this question for some time and am unable to find the required angle. On manually measuring angles, I found that $\angle EDA = 20^{\circ}$, which implies that $\Delta CDE\sim \Delta BFD$. I have tried to prove this result using sine rule but got nowhere. Also, I have checked and there are no cyclic quadrilaterals in this configuration. So, there might be a clever construction that solves this problem. Any solution will be much appreciated. Thanks a lot. Please try not to use values of $\cos 20$ and such in your solution as this may not be provided in contest math.