Angle of triangle

Question

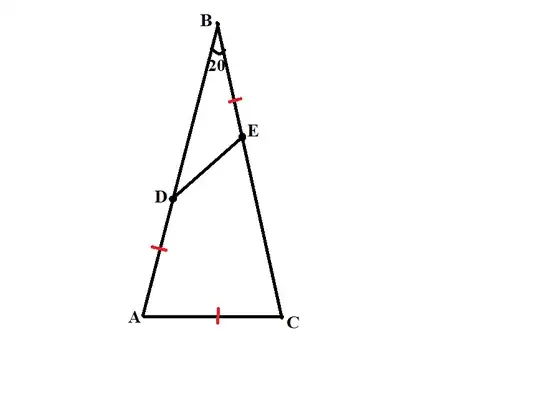
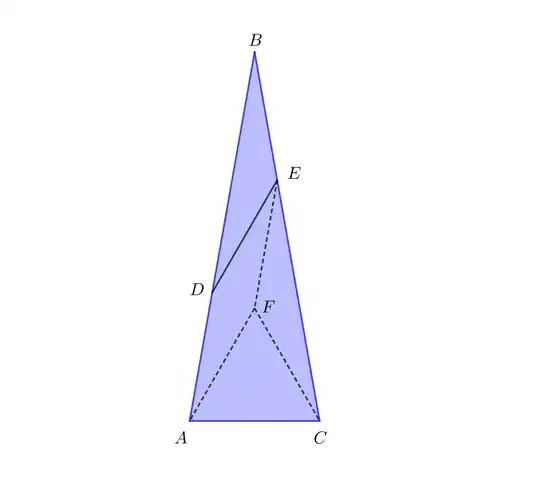
Let $ABC$ be a triangle such that $\angle ABC=20^\circ$, $AB=BC$. Let $D \in AB$, $E \in BC$, $AD=BE=AC$. Find angle $\angle BDE$. Does this problem have a nice geometric solution?

I don't like my trigonometric solution. Let $AC=b$, $AB=a$, $\angle BDE=x$. From triangle $BDE$ we have: $$\frac{b}{\sin x}=\frac{a-b}{\sin\left(20^\circ+x\right)}$$ Then $\sin20^\circ \cot x+\cos20^\circ=\frac{a}{b}-1$. But $$\frac{a}{b}-1=\frac{\sin80^\circ }{\sin20^\circ}-1=2\cos20^\circ $$

Then $\cot x =\cot 20^\circ $. Then $\angle BDE=20^\circ$.

This looks like a variation of Langley's Adventitious Angles. — Deepak, May 23 '21 at 11:28
Does this help you? https://math.stackexchange.com/a/3621501 — , May 23 '21 at 11:32

Jean Marie · Answer 1 · 2021-05-23T21:27:54.130

4

The given figure can be treated as a part of a "bigger figure" i.e., as part of a star-shaped 9-gon:

Fig. 1.

making it accessible to a rather natural proof also based on angle chasing but seemingly in a more logical way.

Two steps:

Step 1: Why is the red triangle in fig. 1 identical to the initial figure ?

$a:=\angle{B}=20°$ because the associated center angle is $2a = 40°=\frac19 360°$,
$BE=AD$ (all the "spikes" of the star are identical),
$AC=AD$ because triangle $ACF$ is equilateral. Indeed $\angle{CAF}=\angle{CAF}=60°$ because they both sustain 3 times arc $a$.

Step 2: Now, let us prove that $\angle{BDE} = 20°$. It follows from the fact that lines $DE$ and $AF$ are parallel, as a consequence of the symmetry of the figure with respect to the axis of symmetry $OG$ where $O$ is the center of the circle.

Remark: The nine-pointed star is an "enneagram (9/4)" if you want to explain at a dinner what you are doing.

edited May 23 '21 at 21:27

answered May 23 '21 at 16:35

Jean Marie

88,997

btw, had the vertex angle been $30^{\circ}$ would we get a hexagon star? – Narasimham May 23 '21 at 18:18
@Narasimham Alas, dealing with the hexagon, you cannot generate a star in this way: the "star of David" is in fact done in two parts (constituted of two triangles). Number $7$ is better behaved... – Jean Marie May 23 '21 at 18:39
Thanks for this clarification.. – Narasimham May 23 '21 at 18:42
Thank you very much! – Witold May 23 '21 at 18:47
nice geometrical approach and explanation ! – G Cab May 23 '21 at 19:47
@G Cab Thanks. This kind of approach should probably be valuable for other problems of this type (some integer angles in degrees + some equalities between lengths). – Jean Marie May 23 '21 at 21:24

dfnu · Accepted Answer · 2021-05-25T08:17:11.103

3

An alternative path with Euclidean geometry. Let $F$ be the point in $\triangle ABC$ such that $\triangle ACF$ is equilateral.

Show that $\triangle BDE \cong \triangle CEF$ (SAS criterion).
Noting that $ABEF$ is an isosceles trapezoid, and therefore $EF\parallel AB$, conclude that $\measuredangle FEC = 20^\circ$.
Obtain the thesis from the fact that $\triangle CEF$ is isosceles and point 1., which yields $ED \cong EB$.

edited May 25 '21 at 08:17

answered May 24 '21 at 21:24

dfnu

8,050

1

Thank you very much! – Witold May 25 '21 at 13:02

score 2 · Answer 3 · answered May 24 '21 at 08:26

Reflect $\triangle ABC$ over line $CA$. Let the reflections of points $D$ and $E$ be $D'$ and $E'$ respectively. Draw $DD'$ and $BD'$.

Observe that $\triangle DCD'$ is equilateral and thereafter quadrilateral $D'DBC$ is a kite.

Hence, $\angle ABD'=\frac {1}{2} \angle DBC=40^{\circ}$. Thus $\triangle ABD'$ is isosceles and thereafter $BD'=AD'$. Also, $AD'=AD=AB-BD=AC-AE=CE$ and hence $BD'=CE$.

Now, observe that, in $\triangle ED'C$ and $\triangle BDD'$, $D'C=DD'$, $CE=BD'$ an $\angle ECD=30^{\circ}=\angle BD'D$ and therefore $\triangle ED'C\cong \triangle BDD'$ by $S-A-S$ criterion of congruence and hence $BD=ED'$.

Also, since $ED'=DE$ and $BD=AE$, $AE=DE$ and therefore $\angle BDE=\angle DAE=20^{\circ}$

Angle of triangle

3 Answers3

Linked