Let $Y1,Y2,...,Y11$ be iid $N(μ,σ^2)$ so that n= 11. Find $P(0.325<S^2/σ^2<2.048)$
My approach was: $P(S^2/σ^2<2.048) - P(S^2/σ^2<0.325)$
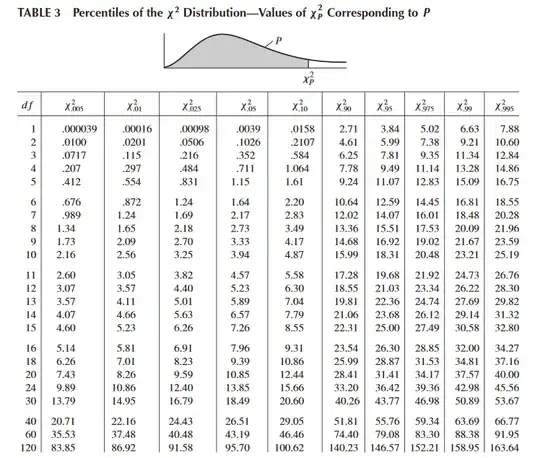
The degrees of freedom would be 10. This is the table I'm attempting to use.
However, I'm not entirely sure where to go from here. I did use R software to get the solution of 0.004040321 - but I don't know if this is correct.