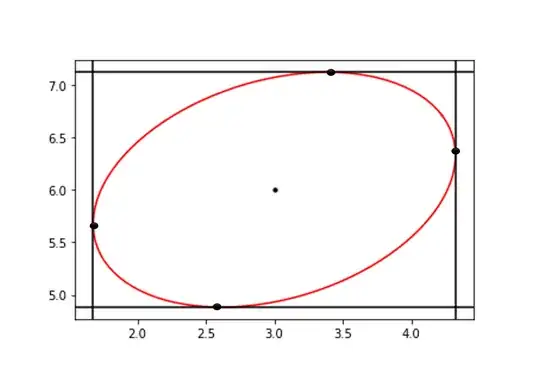
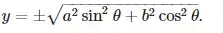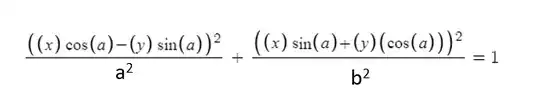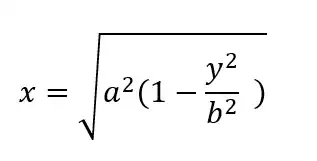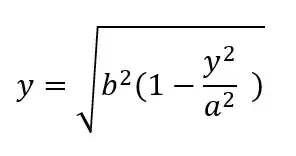Points $(x, y)$ fulfill the rotated ellipse equation
$$\frac{\left( x \cos\theta - y \sin\theta \right)^2}{a^2} + \frac{\left( y \cos\theta + x \sin\theta \right)^2}{b^2} = 1$$
So, substitute $x$ or $y$ with the corresponding maximum,
$$\begin{aligned}
x &= \pm \sqrt{a^2 \cos^2 \theta + b^2 \sin^2 \theta} \\
y &= \pm \sqrt{a^2 \sin^2 \theta + b^2 \cos^2 \theta} \\
\end{aligned}$$
and solve for the other coordinate.
For the right side (positive $x$ boundary), we get
$$\begin{aligned}
x_R &= \sqrt{a^2 \cos^2\theta + b^2 \sin^2\theta} \\
y_R &= \frac{(b^2 - a^2) \sin(2\theta)}{2 \sqrt{a^2 \cos^2\theta + b^2 \sin^2\theta}} \\
\end{aligned}$$
and for the left side (negative $x$ boundary),
$$\begin{aligned}
x_L &= -\sqrt{a^2 \cos^2\theta + b^2 \sin^2\theta} \\
y_L &= -\frac{(b^2 - a^2) \sin(2\theta)}{2 \sqrt{a^2 \cos^2\theta + b^2 \sin^2\theta}} \\
\end{aligned}$$
For the top side (positive $y$ boundary), we get
$$\begin{aligned}
x_T &= \frac{(b^2 - a^2) \sin(2\theta)}{2 \sqrt{a^2 \sin^2\theta + b^2\cos^2\theta}} \\
y_T &= \sqrt{a^2 \sin^2\theta + b^2\cos^2\theta} \\
\end{aligned}$$
and for the bottom side (negative $y$ boundary),
$$\begin{aligned}
x_B &= -\frac{(b^2 - a^2) \sin(2\theta)}{2 \sqrt{a^2 \sin^2\theta + b^2\cos^2\theta}} \\
y_B &= -\sqrt{a^2 \sin^2\theta + b^2\cos^2\theta} \\
\end{aligned}$$
and the axis-aligned bounding box is $(x_L, x_B) - (x_R, y_T)$.
Note that $\sin(2\theta) = \frac{1}{2}\cos(\theta)\sin(\theta)$; you do not need inverse trigonometric functions at all: $a$, $b$, $\cos\theta$, and $\sin\theta$ suffice.
(If the notation is unclear, $\cos^2\theta = ( \cos\theta )^2$.)