Let $R(x)=\frac{P(x)}{Q(x)}$ be a rational function with no poles on the interval $[0,\infty)$, and let $-1<\alpha<1$ be any real number. We wish to calculate the real improper integral
\begin{align}
\int_0^{\infty}x^{\alpha}R(x)\,dx.
\end{align}
For this improper integral to converge, note that since $R(x)$ has no poles on the non-negative real axis, we only have to worry about the appropriate decay conditions at $\infty$. A necessary and sufficient condition for this to occur is that
\begin{align}
\deg (Q)-\deg (P)-\alpha >1.
\end{align}
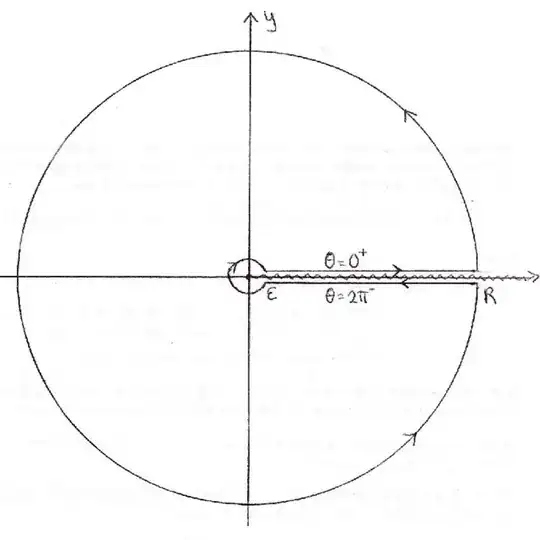
Now, to use the method of residues, we should declare the branch of $z^{\alpha}$ we are using. So, consider the simply connected open set $U=\Bbb{C}\setminus [0,\infty)$, and here we choose the branch of the logarithm such that $0<\arg(z)<2\pi$, and we define $z^{\alpha}:=e^{\alpha \log(z)}$, and we consider the meromorphic function $f(z):= z^{\alpha}R(z)$ defined in $U$. To apply the residue theorem, we have to take a path $\gamma$ lying completely inside the open set $U$. An explicit description of a keyhole contour is as the union of 4 pieces: for large $r>0$ and small $\epsilon>0$, we define
\begin{align}
\begin{cases}
\sigma_1(x):= x +i\epsilon& \text{for $x\in [0,r]$}\\\\
\gamma_1(t):= \sqrt{r^2+\epsilon^2}\,\,e^{it} & \text{for $t\in [\arctan(\epsilon/r), 2\pi - \arctan(\epsilon/r)]$}\\\\
\sigma_{2}(x):= x-i\epsilon&\text{for $0\leq x \leq r$}\\\\
\gamma_{2}(t):= \epsilon e^{it}& \text{for $\frac{\pi}{2}\leq t \leq \frac{3\pi}{2}$}
\end{cases}
\end{align}
And we define $\gamma_{r,\epsilon}:=\sigma_1 + \gamma_1 - \sigma_2 - \gamma_2$, where the signs indicate the orientations of the curves. Here, $\sigma_1$ and $\sigma_2$ are straight line segments just above and below the non-negative real axis, and $\gamma_2$ is a small semicircle of radius $\epsilon$. $\gamma_1$ is then a large circular arc, which "closes up" the curve; this is why it has a funny radius $\sqrt{r^2+\epsilon^2}$ and the parametrization is from $\arctan(\epsilon/r)$ to $2\pi - \arctan(\epsilon/r)$ (be sure to draw a picture).
Now, I went through all this effort to give a very explicit description of the contour $\gamma_{r,\epsilon}$ so that first of all, we can legitimately apply the residue theorem, and second so that it is clear what exactly happens when we take the limits $\epsilon\to 0^+$ and $r\to \infty$. If $\epsilon>0$ is small enough and $r>0$ is large enough then all the poles of $f(z)=z^{\alpha}R(z)$ will lie "inside" the contour, so
\begin{align}
2\pi i \sum \text{Res}(f(z), \text{poles}) &=\int_{\gamma_{r,\epsilon}}f(z)\,dz\\
&=\int_{\sigma_1}f(z)\,dz - \int_{\sigma_2}f(z)\,dz + \int_{\gamma_1}f(z)\,dz-
\int_{\gamma_2}f(z)\,dz\\
&=\int_0^r(x+i\epsilon)^{\alpha}R(x+i\epsilon)\,dx- \int_0^r(x-i\epsilon)^{\alpha}R(x-i\epsilon)\,dx\\
&+\int_{\gamma_1}f(z)\,dz-\int_{\gamma_2}f(z)\,dz
\end{align}
I hope you're convinced that as $\epsilon\to 0^+$ and $r\to \infty$, the intergals over the circular arcs $\gamma_1,\gamma_2$ vanish. So, let us focus on the other two terms.
First, lets focus our attention on $\int_0^r(x+i\epsilon)^{\alpha}R(x+i\epsilon)\,dx$. What happens to the integrand as $\epsilon\to 0^+$? Well it approaches $x^{\alpha}R(x)$, but let's not be too quick and really justify why:
\begin{align}
(x+i\epsilon)^{\alpha}R(x+i\epsilon)&=e^{\alpha \cdot \log(x+i\epsilon)}R(x+i\epsilon)\\
&=e^{\alpha \cdot [\ln |x+i\epsilon|+ i \arg(x+i\epsilon)]}R(x+i\epsilon)\\
&=e^{\alpha\cdot [\ln|x+i\epsilon| + i\arctan(\epsilon/x)]}R(x+i\epsilon),
\end{align}
where in the last line, the argument is as such because by definition it has to lie between $0$ and $2\pi$ (and since $\epsilon>0$, $x>0$). Now, we can use continuity of $\exp$, $\ln$, of $|\cdot|$ and of $\arctan$ to see that as $\epsilon\to 0^+$, the RHS approaches $e^{\alpha\cdot [\ln|x|+0]}R(x)=e^{\alpha \ln x}R(x)=:x^{\alpha}R(x)$, since $x>0$ (we also used the fact that $R$ is a rational function with no poles on the non-negative real axis hence it is continuous there).
For the second integral $\int_0^r(x-i\epsilon)^{\alpha}R(x-i\epsilon)$, we need to be slightly careful:
\begin{align}
(x-i\epsilon)^{\alpha}R(x-i\epsilon)&=e^{\alpha\log(x-i\epsilon)}R(x-i\epsilon)\\
&=e^{\alpha\cdot [\ln|x-i\epsilon|+i(2\pi - \arctan(x/\epsilon))]}R(x-i\epsilon)
\end{align}
As $\epsilon\to 0^+$, we can use continuity of $\exp,\ln,|\cdot|,\arctan$ and of $R$ on the non-negative real axis to deduce that the RHS approaches $e^{\alpha \cdot[\ln x + 2\pi i \alpha]}R(x)=e^{2\pi i \alpha}\cdot x^{\alpha}R(x)$.
So, you see it is this extra factor of $e^{2\pi i \alpha}$ which is what prevents the cancellation (unless $\alpha=0$, in which case our original integral is just $\int_0^{\infty}R(x)\,dx$, and this intergal cannot be evaluated by this method). Now, we can for instance appeal to dominated convergence to justify the interchange of limits and integrals to finally deduce that
\begin{align}
2\pi i \sum\text{Res}(z^{\alpha}R(z),\text{poles}) &=\int_0^{\infty}x^{\alpha}R(x)\,dx - \int_0^{\infty}e^{2\pi i \alpha}x^{\alpha}R(x)\,dx\\
&=(1-e^{2\pi i \alpha})\int_0^{\infty}x^{\alpha}R(x)\,dx
\end{align}
Or equivalently, if $\alpha\neq 0$, we can divide both sides to get
\begin{align}
\int_0^{\infty}x^{\alpha}R(x)\,dx &=\frac{2\pi i}{1-e^{2\pi i \alpha}}\sum\text{Res}(z^{\alpha}R(z)\,\text{poles})
\end{align}
Also, at this stage one should be mindful when calculating residues that $z^{\alpha}$ has been defined such that $0<\arg(z)<2\pi$.
To summarize: the integrals do NOT cancel (unless $\alpha=0$) because although we have an integral $\int_0^{\infty}+\int_{\infty}^0=\int_0^{\infty}-\int_0^{\infty}$ in the end, the integrands are DIFFERENT (unless $\alpha=0$).
Also, contour integrals work the same in the complex plane as they do in $\Bbb{R}^3$ or in $\Bbb{R}^n$. In every case, integrating over a path $\gamma$ and then adding the integral over the oppositely oriented path $-\gamma$ will of course yield $0$, provided you're integrating the SAME object (differential form technically). Otherwise, your argument is equivalent to saying something along the lines of $\int_0^1(1)\,dx + \int_1^0(-1)\,dx = 0$ simply because we're integrating in opposite directions. This is blatantly false; yes we're integrating in opposite directions, but we're integrating different things in different directions.
What made the above computation work out for us is that we took a one-sided limit $\epsilon\to 0^+$, so it MATTERS whether we have $(x+i\epsilon)^{\alpha}$ or $(x-i\epsilon)^{\alpha}$; afterall, that's the whole point of branches of the argument and logarithm: they cannot be continuously extended to $\Bbb{C}\setminus\{0\}$, so they will of course in general yield different limits (in our case we picked up an extra factor of $e^{2\pi i \alpha}$) along different paths.
The wikipedia page on the other hand is sloppily written: in their first line $\int_R^{\epsilon}\frac{\sqrt{z}}{z^2+6z+8}\,dz$ is very poor notation. As written this means an integral along the real axis from $R$ to $\epsilon$; it doesn't matter that they use the letter $z$, no matter what letter they use this means a real integral and this will have to equal $-\int_{\epsilon}^R\frac{\sqrt{z}}{z^2+6z+8}\,dz$. But this is not what they meant. They're trying to justify why integrating over the paths $\sigma_1$ and $\sigma_2$ (which is different from integrating on the real axis) yields a different factor (in their case $\alpha=\frac{1}{2}$, so $e^{2\pi i \alpha}=e^{i\pi}=-1$, and this is the $-1$ you're asking about).