Finding an angle in a triangle

Question

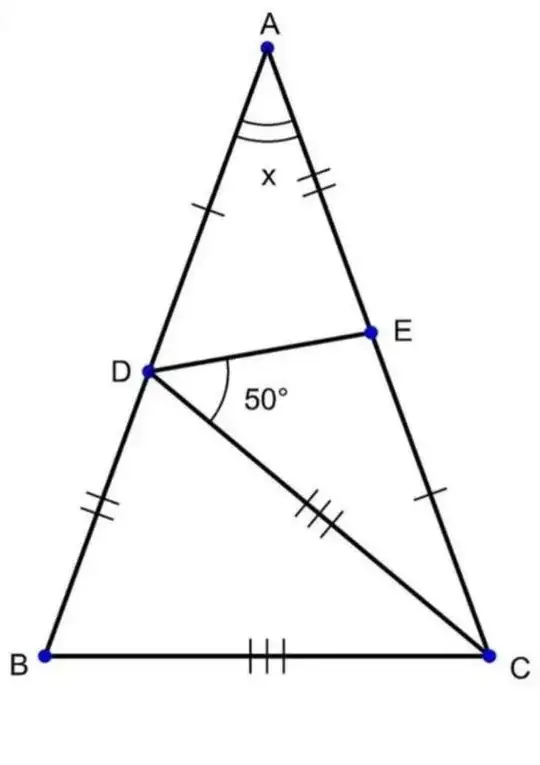
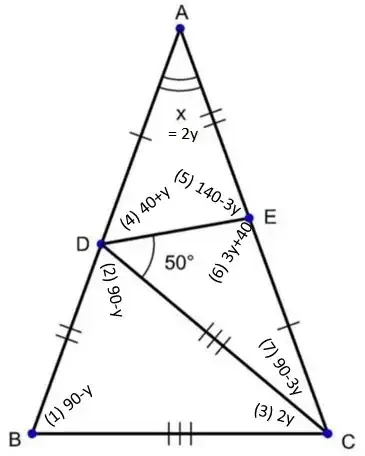
I want to find angle x in this picture.

And this is what I've done so far. Without loss of generality, assume $\overline{\rm BC}=1$

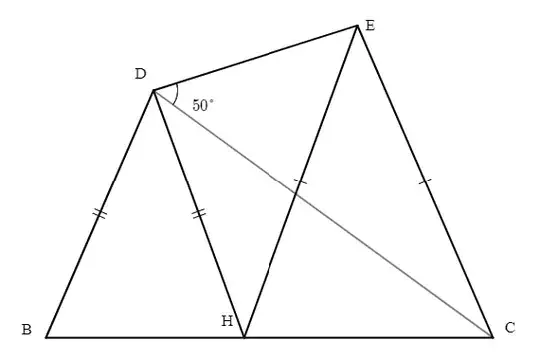
then, $$\overline{\rm BD}= 2\sin{\frac{x}{2}}$$, $$\overline{\rm BH}= 4\sin^2{\frac{x}{2}}= 2(1-\cos{x}), \quad \overline{\rm CH} = 2\cos{x}-1$$ $$\overline{\rm CE}=\frac{2\cos{x}-1}{\sqrt{2-2\cos{x}}}$$ Let $\overline{\rm DE}=y$,

since $\bigtriangleup DCE = \bigtriangleup HCE$, $$\frac{1}{2}y\sin{50^{\circ}}=\frac{1}{2}\sin{x}\frac{(2\cos{x}-1)^2}{2-2\cos{x}}$$ Then by applying law of cosines to $\bigtriangleup DEC$, $$y^2+1-2y\cos{50^{\circ}}=\frac{(2\cos{x}-1)^2}{2-2\cos{x}}$$ So we have a system of equations $$\begin{cases}y\sin{50^{\circ}}=\sin{x}\frac{(2\cos{x}-1)^2}{2-2\cos{x}}\\y^2+1-2y\cos{50^{\circ}}=\frac{(2\cos{x}-1)^2}{2-2\cos{x}} \end{cases}$$ But it's too messy to solve since 50 is not special angle. How can I solve this problem?

Answer 1

Draw a perpendicular on DC from D that intersect AC at E. Draw a circle on C, D and E. Extend BA equal it's measure to get point A'. Connect A' to C. Clearly $\angle A'CB=90^o$. A'C intersect the circle at G. So OG is diameter of the circle. Extend DF to touch the circle at H. Connect H to E. Clearly OG bisects EH and the arc EGH, because:

Let intersection of circle and BC be I, then $arc(EG)=arc (IC)$

$\rightarrow (CE=180)-EG=(GI=180)-GH\rightarrow arc (IH)=arc (CG)\rightarrow\angle GEC=\angle KEI$,also $\angle EIG=\angle ECG$.

Triangle EGC and KEI have two equal angles so their third angles are equale, Sonce $\angle EGC=90^o$ therefore $\angle EKI=90^i$ that is OG is perpendicular on chord EH, so it bisects EH and it's arc EGH, hence G is midpoint of arc EH.

This results in:

$\angle EDG=\angle GDH=\angle ECG$

But $\angle EDH=40^o$, therefore :

$\angle EDG=\angle GDH=\angle ECG=20^o$

Triangle AA'C is isosceles and we have:

$\angle AA'C=\angle ACA'=20^o$

Hence $\angle BAC=40^o$

Answer 2

Draw a perpendicular on CD from D., it touches AC at F. Extend CD. Draw a circle on A and D tangent on CD at D. For this draw perpendicular bisector of AD it intersects the perpendicular on ED at O which is the center of circle.This circle intersects extension of CD at H. Since DF is perpendicular on DH at D , the points F, O and H are on diameter of the circle. In this way $\angle FAH=90^o$ and we have:

$\angle FAH=90^o$

DE is tangent on the circle and $Arc (HD)=2\times 50=100^o$. Hence $\angle DAH=\frac {100}2=50^o$ which results in $\angle BAC=40^o$.

Answer 3

As you are concerned by a trigonometrical solution, here is a direct way to obtain a rather simple equation.

Let $x=2y$.

Fig.1.

Angle chasing on the figure in the order (1)...(6) ((7) being a checking) allows to attribute a value expressed as a function of $y$ to each angle.

Let us apply sine law to triangles ADE and DEC. This will give resp.:

$$\frac{\sin 2y}{\sin (140-3x)}=\frac{DE}{AD} \ \ \text{and} \ \ \frac{\sin (90-3y)}{\sin (50)}=\frac{DE}{EC}$$

As $AD=EC$ we have:

$$\frac{\sin 2y}{\sin (140-3y)}=\frac{\sin (90-3y)}{\sin (50)}$$

which can be simplified into:

$$\frac{\sin 2y}{\cos (50-3y)}=\frac{\cos (3y)}{\sin (50)} \iff \sin 50 \sin 2y=\underbrace{\cos (50-3y)\cos (3y)}_{\tfrac12 \cos(50-6y)+ \tfrac12 \cos(50)}\tag{1}$$

One can verify that $y=20$ degrees is a solution of (1) and check that this solution is the unique one for $y \in (0,90)$ by considering (1) as the equation for the abscissas of the intersection of two curves:

Fig.2: There are apparently 2 solutions to equation (1): $y=20$ degrees and $y=60$ degrees, but the last one is geometrically impossible, due in particular to angle $3y+40$ which would be $>180°$.

But I would like to get a "heuristical" answer by obtaining for example a polynomial equation out of equation (1).

Remark: some similarities with this question.