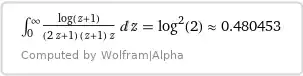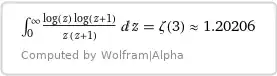Evaluate $\int _0^{\frac{\pi }{2}}x\cot x\ln ^2(\cos x)\:dx$

Question

I want to evaluate $$\int _0^{\frac{\pi }{2}}x\cot (x)\ln ^2(\cos x)\:dx $$ but it's quite difficult. I have tried to rewrite the integral as $$\int _0^{\frac{\pi }{2}}x\cot \left(x\right)\ln ^2\left(\cos \left(x\right)\right)\:dx=\frac{\pi }{2}\int _0^{\frac{\pi }{2}}\tan \left(x\right)\ln ^2\left(\sin \left(x\right)\right)\:dx-\int _0^{\frac{\pi }{2}}x\tan \left(x\right)\ln ^2\left(\sin \left(x\right)\right)\:dx$$ I've also tried to integrate by parts in multiple ways yet I cant go forth with this integral, I also tried using the substitution $t=\tan{\frac{x}{2}}$ but cant get anything to work, I'll appreciate any sort of help.

I also tried using the classical expansion $$\ln \left(\cos \left(x\right)\right)=-\ln \left(2\right)-\sum _{n=1}^{\infty }\frac{\left(-1\right)^n\cos \left(2nx\right)}{n},\:-\frac{\pi }{2}<x<\frac{\pi }{2}$$ But it only gets worse.

Answer 1

An approach in large steps by Jorge Layja. $$\int _0^{\frac{\pi }{2}}x\cot \left(x\right)\ln ^2\left(\cos \left(x\right)\right)\:dx$$

$$=\frac{1}{4}\int _0^{\infty }\frac{\arctan \left(x\right)\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx=\frac{\pi }{8}\int _0^{\infty }\frac{\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx$$ $$-\frac{1}{4}\int _0^{\infty }\frac{\arctan \left(\frac{1}{x}\right)\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx$$

---

$$\int _0^{\infty }\frac{\arctan \left(\frac{1}{x}\right)\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx=\frac{\pi }{2}\int _0^{\infty }\frac{x\ln ^2\left(\frac{x^2}{1+x^2}\right)}{1+x^2}\:dx-\int _0^{\infty }\frac{x\arctan \left(\frac{1}{x}\right)\ln ^2\left(\frac{x^2}{1+x^2}\right)}{1+x^2}\:dx$$ $$=\frac{\pi }{2}\int _0^{\infty }\frac{x\ln ^2\left(\frac{x^2}{1+x^2}\right)}{1+x^2}\:dx-\frac{4}{3}\int _0^{\infty }\frac{x\arctan ^3\left(\frac{1}{x}\right)}{1+x^2}\:dx-\frac{4}{3}\operatorname{\mathfrak{I}} \left\{\int _0^{\infty }\frac{x\ln ^3\left(\frac{x}{x-i}\right)}{1+x^2}\:dx\right\}$$ $$=\frac{\pi }{4}\int _0^1\frac{\ln ^2\left(x\right)}{1-x}\:dx+4\int _0^{\frac{\pi }{2}}x^2\ln \left(\sin \left(x\right)\right)\:dx-\frac{4}{3}\operatorname{\mathfrak{I}} \left\{3\operatorname{Li}_4\left(2\right)+i\pi \ln ^3\left(2\right)-6\zeta \left(4\right)\right\}$$ $$=\frac{5\pi }{4}\zeta \left(3\right)-\frac{\pi ^3}{6}\ln \left(2\right)-\frac{2\pi }{3}\ln ^3\left(2\right)$$

---

Thus. $$\frac{1}{4}\int _0^{\infty }\frac{\arctan \left(x\right)\ln ^2\left(1+x^2\right)}{x\left(1+x^2\right)}\:dx=\frac{\pi }{8}\zeta \left(3\right)-\frac{1}{4}\left(\frac{5\pi }{4}\zeta \left(3\right)-\frac{\pi ^3}{6}\ln \left(2\right)-\frac{2\pi }{3}\ln ^3\left(2\right)\right)$$ Therefore. $$\int _0^{\frac{\pi }{2}}x\cot \left(x\right)\ln ^2\left(\cos \left(x\right)\right)\:dx=-\frac{3\pi }{16}\zeta \left(3\right)+\frac{\pi ^3}{24}\ln \left(2\right)+\frac{\pi }{6}\ln ^3\left(2\right)$$ Thanks to Jorge for showing me this solution.

Answer 2

$$I=\frac{1}{2}\int_0^{\pi/2} x^2\frac{\ln^2\cos x}{\sin^2x} \, dx+\int_0^{\pi/2} x^2{\ln\cos x}\,dx$$ integrating by parts $$\int_0^{\pi/2} x^2 \ln\cos x \, dx=\frac{\pi^3}{24}\ln2-\frac{\pi}{4}\zeta(3)$$ see Integral $\int_0^\pi \theta^2 \ln^2\big(2\cos\frac{\theta}{2}\big)d \theta$. $$I=\int_0^{\pi/2} x^2\frac{\ln^2\cos x}{\sin^2x} \, dx = \frac{1}{4} \int_0^\infty\frac{(\arctan u)^2 \log^2(1+u^2)}{u^2} \, du$$ Put $$x=\arctan u$$

Closer form for $\int_0^\infty\frac{(\arctan{x})^2\log^2({1+x^2})}{x^2}dx$

Answer 3

This is not an answer, Cornel's solution mentioned in comment is already quite elegant. Instead I provide some remarks.

---

Generalizations:

$$\int_0^{\pi/2} x^3 \cot x \log^2(\cos x) \,dx = -3 \pi \operatorname{Li}_5\left(\frac{1}{2}\right)-3 \pi \operatorname{Li}_4\left(\frac{1}{2}\right) \log (2)-\frac{3 \pi^3 \zeta (3)}{32}+\frac{141 \pi \zeta (5)}{64}-\frac{9}{16} \pi \zeta (3) \log^2(2)-\frac{1}{10} \pi \log^5(2)+\frac{1}{8} \pi^3 \log^3(2)+\frac{11}{480} \pi^5 \log (2) $$

$$\int_0^{\pi/2} x \cot x \log^4(\cos x) \, dx = -6 \pi \operatorname{Li}_5\left(\frac{1}{2}\right)-6 \pi \operatorname{Li}_4\left(\frac{1}{2}\right) \log (2)-\frac{3 \pi ^3 \zeta (3)}{32}+\frac{237 \pi \zeta (5)}{64}-\frac{9}{8} \pi \zeta (3) \log^2(2)-\frac{1}{10} \pi \log^5(2)+\frac{1}{4} \pi ^3 \log^3(2)+\frac{19}{480} \pi^5 \log (2)$$ similar evaluations also exist for $\int_0^{\pi/2} x^a \cot x \log^b(\cos x) \log^c(\sin x) \, dx$ with $a$ odd, $b,c$ positive integers with $a+b+c = 5$.

In OP's question, as well as two examples above, we observe that the results are all "divisible by $\pi$" (each term is multiplied by $\pi$). More generally, when $a$ is odd, $$\int_0^{\pi/2} x^a \cot x \log^b(\cos x) \log^c(\sin x) \, dx = \pi \times (\text{Some alternating Euler sums of weight }a+b+c)$$ When $a$ is even, then $\pi$-factor no longer appears, for example $$\int_0^{\pi /2} x^2 \cot x\ln (\cos x) \, \mathrm{d}x = - \frac{\pi^4}{720} + \frac{\ln^42}{24} - \frac{\pi^2\ln^22}{6} + \operatorname{Li}_4\left(\frac{1}{2}\right)$$

Answer 4

A quite elegant solution.

The fact $$ \Im\left[\log^3\left(\frac{1+e^{2ix}}2\right)\right]=3x\log^2\cos x-x^3 $$

yields $$ \int_0^{\pi/2}x\cot x\log^2\cos x~d x=\frac16\Im\left[\int_{-\pi/2}^{\pi/2}\cot x\log^3\left(\frac{1+\text e^{2ix}}2\right)d x\right]+\frac13\int_0^{\pi/2}x^3\cot x~d x $$ The rest two integrals are easy. $$ \begin{align} &\int_{-\pi/2}^{\pi/2}\cot x\log^3\left(\frac{1+\text e^{2ix}}2\right)~d x \\=&\oint\frac{z+1}{z-1}\log^3\left(\frac{1+z}2\right)~\frac{d z}{2iz}\quad z=e^{2ix} \\=&2\pi~\text{Res}\left[\frac{z+1}{z-1}\log^3\left(\frac{1+z}2\right)~\frac{1}{2iz},0\right] \\=&i\pi\log^32 \end{align} $$

The contour is the unit circle with small perturbations near $z=\pm1$ . $$ \begin{align} &\int_0^{\pi/2}x^3\cot x~d x \\=&x^3\log(2\sin x)\Big|_0^{\pi/2}-3\int_0^{\pi/2}x^2\log(2\sin x)d x \\=&\frac{\pi^3}8\log2+3\int_0^{\pi/2}\sum_{n\ge1}\frac{\cos(2nx)}nx^2~d x \\=&\frac{\pi^3}8\log2+3\sum_{n\ge1}\frac{\pi(-1)^n}{4n^3} \\=&\frac{\pi^3}8\log2-\frac{9\pi}{16}\zeta (3) \end{align} $$

Where Fourier series of $\log(2\sin x)$ is applied.

Combine them and the result follows. $$ \int_0^{\pi/2}x\cot x\log^2\cos x~d x=\frac{\pi^3}{24}\log2-\frac{3\pi}{16}\zeta (3)+\frac\pi6\log^32 $$

Answer 5

Below is a real method. Utilize \begin{align} &\int_0^1 \frac{\ln\frac{1-t}t}{1+y^2 t^2} \, \overset{s=\frac{1-t}t }{dt } =\int_0^\infty \frac{\ln s}{(s+1)^2+y^2}\overset{s\to \frac{1+y^2}s}{ds}\\ &\hspace{5mm} =\frac12 \int_0^\infty \frac{\ln(1+y^2)}{(s+1)^2+y^2}\ ds = \frac1{2y}\tan^{-1}y\ \ln(1+y^2) \end{align} to integrate as follows \begin{align} &\hspace{5mm}\int_0^{\frac\pi2} x \cot x\ln^2(\cos x) \overset{y=\tan x} {dx}\\ & =\dfrac14\int_0^\infty\,\dfrac{ \tan^{-1} y \ \ln^2\left(1+y^2\right)}{y(1+y^2)}dy\\ &= \frac12 \int_0^\infty \frac{\ln(1+y^2)}{1+y^2}\int_0^1\frac{\ln\frac{1-t}t}{1+y^2t^2}dt \ dy\\ &= \frac12 \int_0^1\int_0^\infty \frac{\ln\frac{1-t}t }{1-t^2}\left(\frac{\ln(1+y^2)}{1+y^2}-\frac{t^2 \ln(1+y^2)}{1+y^2t^2}\right)dy \ dt\\ &= \frac\pi2 \int_0^1 \frac{\ln\frac{1-t}t}{1-t^2} \left(\ln2 -t \ln\frac{1+t}t \right)dt \\ &= \frac\pi2 \int_0^1 \frac{\ln2\ln\frac{1-t}t-t \ln(1-t)\ln(1+t)}{1-t^2} \overset {t\to \frac{1-t}{1+t}}{dt}\\ &\hspace{10mm}+\frac\pi2\int_0^1 \frac{t\ln t\ln(1-t^2)}{1-t^2} \overset{1-t^2\to t^2}{dt}-\frac\pi2\int_0^1 \frac{t\ln^2t}{1-t^2} \ \overset{ibp}{dt}\\ &= \frac\pi4 \int_0^1 \frac{2\ln^2\frac{1+t}2}{1+t}-\frac{\ln2\ln(1-t)}{t} +\frac{\ln t\ln(1-t)}{t}\ dt\\ &=\frac\pi4 \left[\frac23 \ln^32-\ln2\left(-\frac{\pi^2}{6}\right)-\frac34\zeta(3)\right]\\ &= \frac{\pi }{6}\ln ^32+ \frac{\pi ^3}{24}\ln 2-\frac{3\pi }{16}\zeta (3) \end{align}

Answer 6

$\color{green}{\textbf{Version of 15.05.21.}}$

$\color{brown}{\textbf{Primary transformations.}}$

Substitution in the form of $$x=\arctan y,\quad \cos^2 x=\dfrac1{1+y^2},\quad \cot x = \dfrac1y,\quad \text dx = \dfrac{\text dy}{1+y^2}\tag1$$ presents the given integral in the form of $$I=\int\limits_0^{\large\frac\pi2} x \cot x\ln^2(\cos x)\,\text dx =\dfrac14\int\limits_0^\infty \arctan y \ln^2\left(1+y^2\right)\,\dfrac{\text dy}{y(1+y^2)}\tag2.$$ This allows partitionally use my answer to the similar question.

Is known the integral $$\int\limits_0^\infty\dfrac{\ln x\,\text dx}{(x+a)(x+b)} =\dfrac{\ln^2a-\ln^2b}{2a-2b},\quad(\Re a>0,\;\Re b>0).\tag3$$

Then $$\dfrac1y\arctan y\ln(1+y^2) = \dfrac i{2y}(\ln(1-iy)-\ln(1+iy))(\ln(1-iy)+\ln(1+iy))$$ $$ = 2\,\dfrac{\ln^2(1-iy)-\ln^2(1+iy)}{2(1-iy)-2(1+iy)} = 2\int\limits_0^\infty\dfrac{\ln z\,\text dz}{(z+1-iy)(z+1+iy)},$$ $$\dfrac1y\arctan y\ln(1+y^2)= 2\int\limits_0^\infty\dfrac{\ln z\,\text dz}{(z+1)^2+y^2}.\tag4$$ Besides, for $\;p>0\;$ $$\int\limits_0^\infty \dfrac{\ln(1+y^2)\,\text dy}{p^2+y^2} =\pi\,\dfrac{\ln(p+1)}{p}.\tag5$$

Taking in account $(2)-(5),$ one can get $$I = \dfrac12\int\limits_0^\infty\int\limits_0^\infty \dfrac{\ln z}{(z+1)^2+y^2} \dfrac{\ln(1+y^2)}{1+y^2}\,\text dz\,\text dy$$ $$= \dfrac12\int\limits_0^\infty\int\limits_0^\infty \left(\dfrac1{1+y^2}-\dfrac1{(z+1)^2+y^2} \right)\ln(1+y^2)\,\dfrac{\ln z}{z^2+2z}\,\text dy\,\text dz,$$ $$I= \dfrac\pi2\int\limits_0^\infty \left(\ln 2-\dfrac{\ln(z+2)}{z+1}\right)\,\dfrac{\ln z}{z^2+2z}\,\text dz.\tag6$$

Considered transformations allowed to simplify the given integral. However, the obtained integral looks non-trivial too.

$\color{brown}{\textbf{Splitting.}}$

Integral $(6)$ can be splitted to the six integrals. Really, taking in account $(3),$

\begin{align} &\dfrac4\pi\,I= 2\int\limits_0^\infty \dfrac{(z\ln 2-\ln(1+\frac12z))\ln z}{z(1+z)(2+z)}\,\text dz\\[4pt] &= 2\ln2\int\limits_0^\infty \dfrac{\ln z}{(1+z)(2+z)}\,\text dz -\int\limits_0^\infty \dfrac{\ln(2z) \ln(1+z)}{z(1+z)(1+2z)}\,\text dz\\[4pt] &= \ln^3 2 -\int\limits_0^\infty \dfrac{\ln(2) \ln(1+z)}{z(1+z)(1+2z)}\,\text dz -\int\limits_0^\infty \dfrac{\ln(z) \ln(1+z)}{z(1+z)}\,\text dz +2\int\limits_0^\infty \dfrac{\ln(z) \ln(1+z)}{(1+z)(1+2z)}\,\text dz\\[4pt] &= \ln^3 2 -\int\limits_0^\infty \dfrac{\ln(2) \ln(1+z)}{z(1+z)(1+2z)}\,\text dz -\int\limits_0^\infty \dfrac{\ln(z) \ln(1+z)}{z(1+z)}\,\text dz\\[4pt] &+\int\limits_0^\infty \dfrac{\ln^2(1+z)}{(1+z)(1+2z)}\,\text dz +\int\limits_0^\infty \dfrac{\ln^2(z)}{(1+z)(1+2z)}\,\text dz -\int\limits_0^\infty \dfrac{(\ln(z+1)-\ln z)^2}{(1+z)(1+2z)}\,\text dz. \end{align}

$\color{brown}{\textbf{Closed forms of the integrals.}}$

Four first interals of the five can be calculated by Wolfram Alpha immediately, \begin{align} &I_1 = -\int\limits_0^\infty \dfrac{\ln(2) \ln(1+z)}{z(1+z)(1+2z)}\,\text dz = -\ln^2 2,\\[4pt] &I_2 = -\int\limits_0^\infty \dfrac{\ln(z) \ln(1+z)}{z(1+z)}\,\text dz = -\zeta(3),\\[4pt] &I_3 = \int\limits_0^\infty \dfrac{\ln^2(1+z)}{(1+z)(1+2z)}\,\text dz = \dfrac1{12}(21\zeta(3)+4\ln^3 2 -\pi^2 \ln4),\\[4pt] &I_4 = \int\limits_0^\infty \dfrac{\ln^2(z)}{(1+z)(1+2z)}\,\text dz = \dfrac13\,\ln2(\pi^2+\ln^2 2). \end{align}

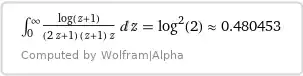
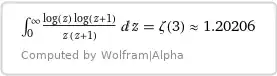
Besides, $$I_5 = -\int\limits_0^\infty \dfrac{(\ln(z+1)-\ln z)^2}{(1+z)(1+2z)}\,\text dz = -\int\limits_0^\infty \dfrac{\ln^2\left(\dfrac1z+1\right)}{z^2\left(1+\dfrac1z\right)\left(2+\dfrac1z\right)}\,\text dz,$$ $$I_5 = -\int\limits_0^\infty \dfrac{\ln^2(z+1)}{(1+z)(2+z)}\,\text dz = -\frac32\,\zeta(3).$$

Therefore, $$\dfrac4\pi I = \ln^3 2 - \ln^3 2 - \zeta(3) + \dfrac1{12}(21\zeta(3)+4\ln^3 2 -\pi^2 \ln4) + \dfrac13\,\ln2(\pi^2+\ln^2 2) -\dfrac32\,\zeta(3),$$ $$\color{green}{\mathbf{I = \dfrac\pi{6}\,\ln^3 2 - \dfrac{3\pi}{16}\,\zeta(3) + \dfrac{\pi^3}{24}\ln2.}}\tag7$$