Limits of negative-power tower

Question

Consider the following: $$n \uparrow -\Bigl((n+1) \uparrow -\bigl((n+2) \uparrow \cdots \uparrow -m \bigr)\Bigr)= n^{{{-(n+1)}^{-(n+2)}}^{\cdots^{-m}}}$$ It doesn't converge for $m \to \infty$, but eventually alternates between two values where the larger one occurs at even numbers of exponents because for $x \to \infty : n^{-x^{-x}} \approx n^0 > n^{-(n+1)^{-x^{-x}}} \approx n^{-1}$.

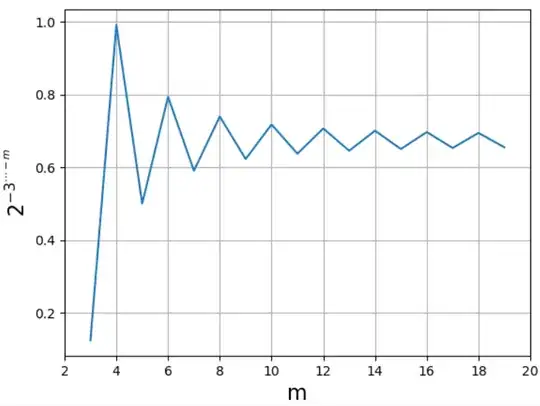$\qquad$

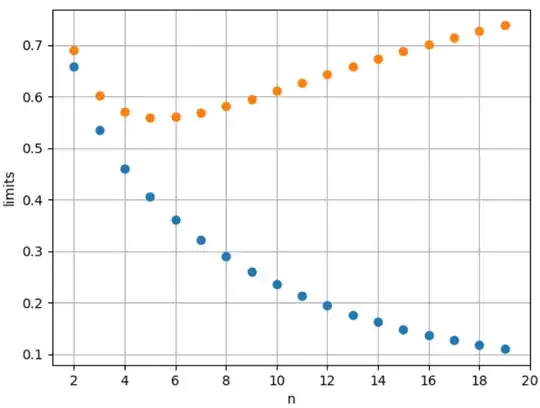
For $2^{-3^{-4^{-5^\cdots}}}$ the limits are for example about $0.6903471$ and $0.6583656$.

Is there a closed form for the two limits of the power tower? Are the limits always irrational?

Thanks in advance.

Answer 1

This will be an attempt at a semi closed form by using logarithm properties. The fraction MathJax will not be used for better viewing let this number, odd or even limit, be called $C$ for constant: \begin{align} C&=(1/2)^{{1/3}^{{\ldots}^{1/n}}}\\&=\exp\biggr(\ln\biggr((1/2)^{{1/3}^{{\ldots}^{1/n}}}\biggr)\biggr)\\&= \exp\bigr({{1/3}^{{\ldots}^{1/n}}}\times -\ln(2)\bigr)\\&= \exp\bigr(\exp\bigr({1/4}^{{\ldots}^{1/n}}\times-\ln(3)\bigr)\times-\ln(2)\bigr)\\&=\exp(\exp(\ldots(-\ln(n))\times-\ln(n-1))\ldots\times-\ln(3))\times-\ln(2))\end{align}

This means our final answer is: $$C=\lim_{n\to \infty} \exp(\exp(\ldots(-\ln(n))\times-\ln(n-1))\ldots\times-\ln(3))\times-\ln(2)).$$

These $e^y$ can also be expressed in terms of a power infinite summation series for the simplest sum. You can also turn the $\exp(y)$ into $e^y$ to see the full conventional shape of the number. I am not too sure how to proceed from here. Maybe I will think of something else. Please give me feedback and correct me!