What is the value of $\left(\frac{1}{2}\right)^{\left(\frac{1}{3}\right)^{\left(\frac{1}{4}\right)^{\unicode{x22F0}}}}$?

Question

Motivation

I have been thinking about this thing for quite a while now. I have tried many ways but couldn't really figure it out.

I am pretty sure that this kind of expressions don't really have a closed form, so I am asking for other representation for example maybe in terms of an infinite sum or product or something.

Creating A New Notation

Just like there is a notation for a sum $\textstyle\displaystyle{\sum_{n=a}^{b}s_n=s_a+\cdots+s_b}$ and also for a product $\textstyle\displaystyle{\prod_{n=a}^{b}s_n=s_a\cdots s_b}$, I was quite surprised that there wasn't any notation for exponentiation.

I would agree that there wouldn't be any use for this notation but still, why would no mathematician ever would create such a notation just for the sake of curiosity. That is why I would request readers to give me any references if there are any. I haven't found any, so I am creating my own. Let $$\boxed{\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=a}^{b}s_k=s_a^{\unicode{x22F0}^{s_b}}}}$$ where $b>a$. If $a>b$ then $\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=a}^{b}s_k=1}$ and $\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=a}^{b}x=^{b-a+1}x}$. Obviously $a,b\in\mathbb{Z}$.

Unlike product and sum, exponentiation isn't commutative so we have to be careful when using the notation. Maybe we can modify it a little bit to include the ordering.

By the way we are defining $\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=a}^{\infty}s_k:= \lim_{n\rightarrow\infty}\left({\huge\varepsilon\normalsize}_{k=a}^{n}s_k\right)}.$

Some Natural Questions

When written out in the form of this notation, some natural curious questions arrive or at least some arrived in my mind, for example $\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=2}^{\infty}\frac{1}{k^s}}$ and $\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=2}^{\infty}\frac{1}{n}}$.

My Curiosity

My initial curiosity was $H=\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=2}^{\infty}\frac{1}{k}=\left(\frac{1}{2}\right)^{\left(\frac{1}{3}\right)^{\left(\frac{1}{4}\right)^{\unicode{x22F0}}}}}$.

As pointed out by Tavish in the comments, this can be written as a recurrence relation given by $$\textstyle\displaystyle{a_{n+1}=-\frac{\ln(a_n)}{\ln(n)}}$$ where $\textstyle\displaystyle{a_n=\left(\frac{1}{n}\right)^{\left(\frac{1}{n+1}\right)^{\unicode{x22F0}}}}$. Solving this will help us derive $H$.

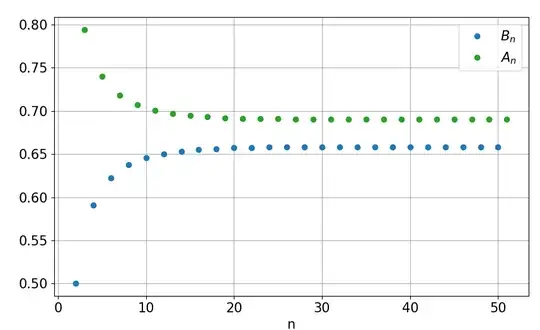
But as pointed out in the comments and in this question (Note that this question focuses on the convergence of $H$, while my question focuses on something different), $H$ doesn't really make much sense by the definition of infinite power tower above because it seems that $$\textstyle\displaystyle{\lim_{n\rightarrow\infty}\left({\huge\varepsilon\normalsize}_{k=2}^{2n}\frac{1}{k}\right)\neq\lim_{n\rightarrow\infty}\left({\huge\varepsilon\normalsize}_{k=2}^{2n+1}\frac{1}{k}\right)}.$$ In particular, we have

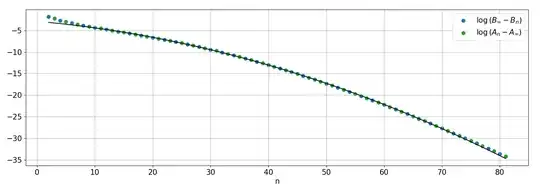
\begin{align}H_O&=\lim_{n\rightarrow\infty}\left({\huge\varepsilon\normalsize}_{k=2}^{2n+1}\frac{1}{k}\right)=0.6903471261\cdots\\H_E&=\lim_{n\rightarrow\infty}\left({\huge\varepsilon\normalsize}_{k=2}^{2n}\frac{1}{k}\right)=0.6583655992\cdots\end{align}

Let $E_n=\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=2}^{2n}\frac{1}{k}}$ and $O_n=\textstyle\displaystyle{{\huge\varepsilon\normalsize}_{k=2}^{2n+1}\frac{1}{k}}$. I tried constructing a recurrence relation for $E_n$ and $O_n$, but couldn't, except \begin{align}E_{n+1}&=\left(\log_{\frac{1}{2n-1}}(\cdots\log_{\frac{1}{2}}(E_n))\right)^{\left(\frac{1}{2n+1}\right)^{\left(\frac{1}{2n+2}\right)}}\\O_{n+1}&=\left(\log_{\frac{1}{2n}}(\cdots\log_{\frac{1}{2}}(O_n))\right)^{\left(\frac{1}{2n+2}\right)^{\left(\frac{1}{2n+3}\right)}}\end{align} which is not really workable. If there is a way to simplify it then please do tell me or write a partial answer about it, because it would help us a lot in finding the values of $H_E$ and $H_O$.

My Question

I am pretty sure that there really isn't closed form of $H_E$ and $H_O$.

So I am asking for a different representation for those constants, maybe as a sum or an integral possibly?

Answer 1

It is possible to write the expression as a series. Help on a literature search from a Discord maths server led to the following paper

Bender CM, Vinson JP. Summation of power series by continued exponentials. J. Math. Phys. 37, 4103 (1996).

where the function $a_0\exp(a_1z\exp(a_2z\exp(\cdots)))$ was discussed. A Taylor series expansion is given in equation (1.3) as $$a_0+\sum_{n\ge1}\sum_{j_1+\cdots+j_k=n}\left(\prod_{i=1}^k\frac{a_0(a_ij_{i-1})^{j_i}}{j_i!}\right)z^n$$ where $j_0=1$ and $j_i>0$ for each $i\ge1$ (a multinomial sum of sorts). Evidently, given a particular value of $z$, this function converges if the sequence of exponential convergents $a_0,a_0\exp(a_1z),\cdots$ converges. However, as shown in Convergence of $a_n=(1/2)^{(1/3)^{...^{(1/n)}}}$, our sequence converges to two distinct values subsequenced by parity, so the results in the paper do not immediately apply.

Considering the even case first (the sequence $E_n$ in your notation), we can get round this by taking the function $a_0\exp(a_1\exp(a_2z\exp(a_3\exp(a_4z\exp(\cdots)))))$ instead, where the indeterminate $z$ occurs only at even indices of $a_m$. The coefficients are such that $a_0=1$ and $a_m=-\log(m+1)$ for each $m\ge1$ and eventually we will take $z=1$ to evaluate the expression.

Writing $f_k(z)=\exp(a_{2k+1}\exp(a_{2k+2}zf_{k+1}(z)))$ for each $k\ge0$, we obtain \begin{align}\small f_0(z)&\small=e^{a_1}\left(1+a_1\left(a_2zf_1(z)+\frac{a_2^2}2z^2f_1(z)^2+\cdots\right)+\frac{a_1^2}2\left(a_2zf_1(z)+\frac{a_2^2}2z^2f_1(z)^2+\cdots\right)^2+\cdots\right)\\\small f_1(z)&\small=e^{a_3}\left(1+a_3\left(a_4zf_2(z)+\frac{a_4^2}2z^2f_2(z)^2+\cdots\right)+\frac{a_3^2}2\left(a_4zf_2(z)+\frac{a_4^2}2z^2f_2(z)^2+\cdots\right)^2+\cdots\right)\end{align} and so on. The first few coefficients of $z^n$ in $f_0(z)$ are as follows \begin{align}[z^0]&=e^{a_1}\\ [z^1]&=e^{a_1}a_1a_2e^{a_3}\\ [z^2]&=e^{a_1}a_1a_2e^{a_3}a_3a_4e^{a_5}+e^{a_1}a_1\frac{a_2^2}2e^{2a_3}+e^{a_1}\frac{a_1^2}2a_2^2e^{2a_3}\\ [z^3]&=\tiny e^{a_1}a_1a_2e^{a_3}\left(a_3\frac{a_4^2}2e^{2a_5}+\frac{a_3^2}2a_4^2e^{2a_5}\right)+e^{a_1}a_1\frac{a_2^2}2\cdot2e^{a_3}a_3a_4e^{a_5}+e^{a_1}a_1\frac{a_2^3}6e^{3a_3}+e^{a_1}\frac{a_1^2}2a_2^3e^{3a_3}+\frac{a_1^3}6a_2^3e^{3a_3}.\end{align} We note that the coefficients are much less elegant that those in the function considered in the paper, because dropping the indeterminate $z$ results in irregular contributions when extracting each term. I don't have time at this moment to attempt a closed form expression, but it seems likely that there is one (in the form of a double multinomial sum). And from which we immediately have $H_E=\sum\limits_{i\ge0}[z^i]$.

We can proceed with the odd case in a very similar way by taking the function $\exp(a_1z\exp(a_2\exp(a_3z\exp(\cdots))))$ and the sum of its coefficients will give us $H_O$.

Answer 2

$\hspace{3.5cm}$

Using your notation, define $\overset{n}{\underset{k=2}{\huge \varepsilon}} \, \frac{1}{k} = A_n$ if $n$ is odd and $B_n$ if $n$ is even. We can subtract the limits from each "branch" and flip the lower one to be able to perform one regression on the logarithm of the sequence:

For $n > 10$ the sequence is approximated pretty well by

$$ f(n) = \exp (-0.0034n^2 - 0.117n - 2.912) \qquad \to \begin{matrix} A_n = f(n) + A_\infty \\ B_n = B_\infty - f(n) \end{matrix} $$

By the way, the recursion is pretty useless because it starts at $n = \infty$ and $a_2 = - \frac{\ln a_1}{\ln 1}$ which is not determined.

Answer 3

I will use my same answer as in Christian’s post. Better a form that none. This will be an attempt at a semi closed form by using logarithm properties. The fraction MathJax will not be used for better viewing let this number, odd or even limit, be called C for constant. Note that these represent both cases of $C=\text H_{e,o}$: $$C=(1/2)^{{1/3}^{{...}^{1/n}}}=\exp\biggr(\ln\biggr((1/2)^{{1/3}^{{...}^{1/n}}}\biggr)\biggr)= \exp\bigr({{1/3}^{{...}^{1/n}}} \cdot -\ln(2)\bigr)= \exp\bigr(\exp\bigr({1/4}^{{...}^{1/n}} \cdot-\ln(3)\bigr) \cdot-\ln(2)\bigr)=\exp(\exp(…(-\ln(n)) \cdot-\ln(n-1))… \cdot-\ln(3)) \cdot-\ln(2))$$

This means our final answer is: $$C=\lim_{n\to \infty} \exp(\exp(…(-\ln(n)) \cdot-\ln(n-1))… \cdot-\ln(3)) \cdot-\ln(2)) = \lim_{n\to \infty} e^{e^{e^{{.^{.^.}}^{(-\ln(n)) \cdot-\ln(n-1)}…\cdot-\ln(3)} \cdot-\ln(2)}}$$

Here is an attempt at a differential equation using a similar process. I will differentiate the general version which may combine both cases:

$$y(x)=2^{{-3}^{{-4}^{.^{.^{.^{{(x-1)}^x}}}}}}= 2^{{-3}^{{-4}^ {{.^{.^.}}^{g(x)}}}}$$

Let’s differentiate to try and find a differential equation:

$$y’=y’(x)=\frac d{dx} \exp \ln\left( 2^{{-3}^{{-4}^ {{.^{.^.}}^{g(x)}}}}\right) =\frac d{dx}\exp\left((-3)^{{-4}^{{-5}^ {{.^{.^.}}^{g(x)}}}}\ln(2)\right)=2^{-3^{{-4}^{{-5}^ {{.^{.^.}}^{g(x)}}}}}\ln(2)\frac d{dx} -\exp\left( {{-4}^{{-5}^ {{.^{.^.}}^{g(x)}}}}\ln(3)\right)= -2^{-3^{{-4}^{{-5}^ {{.^{.^.}}^{g(x)}}}}} 3^{-4^{{-5}^{{-6}^ {{.^{.^.}}^{g(x)}}}}}\ln(2)\ln(3)\frac d{dx} 4^{{-5}^{{-6}^ {{.^{.^.}}^{g(x)}}}}=-y\log_2(y)\ln(2)\ln(3)\frac d{dx} \log_2(\log_3(y))=-\ln(2)y\frac d{dx}\log_2(y)= \ln(2)y\frac{y’(x)}{\ln(2)y}=y= … $$

However, this produces a true expression. Trying to differentiate @Tavish’s $a_n=\left(\frac1n\right)^{\left(\frac1{n+1}\right)^…}$ produces an increasingly complicated derivative, so no functional equation not differential equation can be made so far to try and find a value of $\text H_{e,o}$.

Let me think of something else. This also looks like another recurrence relation. Please correct me and give me feedback!